大家好，我是钱哥，我来写一下 PKUSC2024 最短路径 的题解。没有做过这个题的同学可以先自行做一做。

我们下面来讲解一下如何一步步解决这个题目。

subtask 4

首先，我们来解决第一个具有挑战性的子任务：$m \leq 2.5 n$，这个点具有一个比较显然的性质，点的度数不大。

大家来发挥一下想象力，由一个点 $s$ 为根最短路树，几乎是以指数级展开的，因此，我们可以联想到我们普及组就学习过的算法：折半搜索。

在这个题上，我们可以执行双向 dijkstra，由 $s$ 与 $t$ 分别开始 dijkstra（当然，$t$ 在反图上跑）。

当两个点的 dijkstra 相遇了，我们找到了最短路吗？很可惜，并没有。

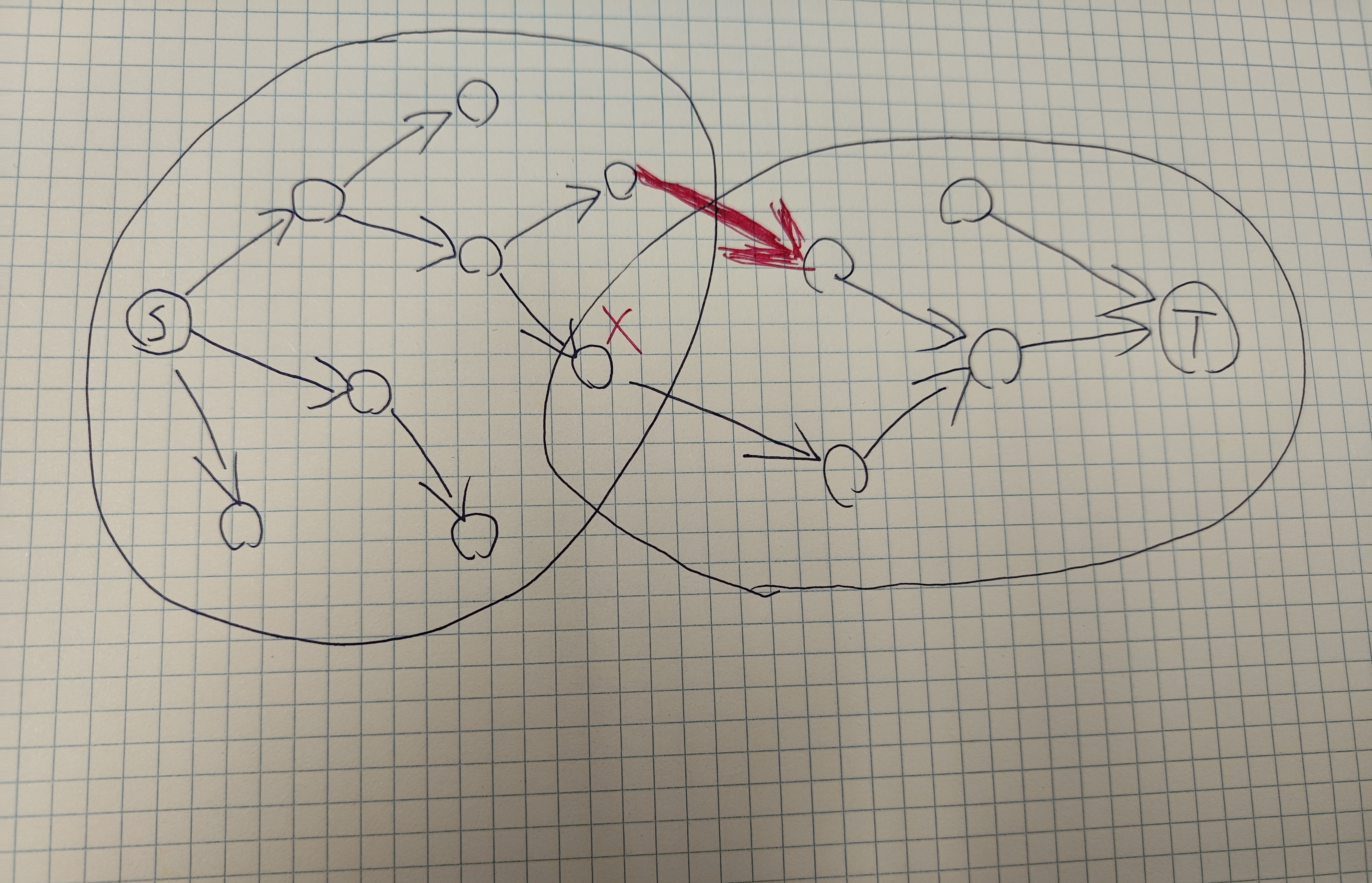
我们发现，即使两边的 dijkstra 相遇在了 $x$，经过红色边的路径依旧可能是最短路径。

好在，我们简单分析一下，我们可以发现两边相遇过后，最多有一条不在最短路上的边。因此，我们可以枚举一侧的点，枚举它的出边，找到所有可能的路径。

现在我们来分析一下我们算法的复杂度，假设我们双向 dijkstra 一共访问了 $S$ 个点，如果所有点度数比较平均，那么它们度数都是 $O(m/n)$ 的，那么经过不严谨的猜测，我们整个算法的复杂度为：$O(S * m/n + S \log S)$，其中前者是我们 dijkstra 需要松弛的边数（也是我们枚举红色边的条数），后者是堆。

那么问题来了，$S$ 可以控制到多大呢？

双向 dijkstra

我们来分析一下 dijkstra 的行为：

q.emplace(0, S);
while (!q.empty()) {
  auto [d, u] = q.top(); q.pop();
  if (dis[u] != -1) continue;
  dis[u] = d;
  for (auto [v, w] : e[u]) {
      q.emplace(d + w, v);
  }
}

这份 dijkstra 可能和大家写法并不完全相同，但是完全可以看出是正确的 dijkstra。我们其实可以看到，每条边的目标点，事实上只有在第 $4$ 行才第一次被用到（尽管它可能很早就在堆里了），在这之前，它完全不会影响整个代码的运行。因此，事实上每次到第 $4$ 行时候，$u$ 都是一个在 $[1, n]$ 中均匀独立随机生成的变量！

如果你仔细思考一下，你会发现，在双向 dijkstra 相遇之前，事实上两边也是互相独立的。因此，这个过程就像生日悖论一样，如果每次扩展最短路树上点少的一侧，期望只要扩展 $O(\sqrt{n})$ 次，我们就可以找到相遇的点。

除此之外，我们可以发现，最短路树的点之间的所有边也是 $O(\sqrt{n})$ 条（事实上，每次一个元素出堆就对应了一条边，而不是一个点）。

让我们回到 subtask 4，我们可以发现，此时这个算法的时间复杂度大约为 $O(\sqrt{n} \log{n})$，这足以让我们通过这个子任务。

subtask 2

相信你发现了，上面的算法甚至没有办法通过子任务 $2$。虽然这个子任务是给大家各显神通的，但是如果你仔细思考，你就会发现度数在整个题目的影响是非常大的。下面我们来介绍，如何处理 dijkstra 中，每个点度数很大，导致松弛边过多。

如果你做过 $k$ 短路，或者类似的题，它们都有用到这个技巧：我们注意到由一个点出发的边，肯定是边权小的会先出堆，因此，如果我们预先将每个点的出边按照边权排序，我们可以只往堆中塞入第一条边，当第一条边出堆时候，再把第二条边塞入堆中。如此操作，堆中的边数就线性于出堆次数了，我们也就解决了这个艰难的问题。

你也许想问，到这里，我们还是没有解决枚举中间边的复杂度，事实上，这个子任务我们只要跑单向 dijkstra 就可以了（×），因为每次到的点是独立均匀随机的，因此只有期望 $O(n)$ 次堆操作，所以复杂度为 $O(qn\log n + m \log m)$（如果你写了这个算法被卡常了，那我对不起你 ）。

最终算法

下面我们要迎接我们的最终算法了，非常精彩！

我们现在已经可以用 $O(\sqrt{n} \log{n})$ 的期望时间跑出相遇点了，我们下面要处理如何快速找到可能的中间边的问题。

我们考虑一下这条路径：$s \rightarrow a \color{red}{\rightarrow} b \rightarrow t$，它的距离是 $dist_{s, a} + e_{a, b} + dist_{b, t}$，而我们知道，$dist_{s, a} \leq dist_{s, x}, dist_{b, t} \leq dist_{x, t}$，因此，我们这条边肯定不能太长，$e_{a, b} \leq (dist_{s, x} - dist_{s, a}) + (dist_{x, t} - dist_{a, t})$，显然，$e_{a, b} \leq 2 \max(dist_{s, x} - dist_{s, a}, dist_{x, t} - dist_{a, t})$，我们考虑在大的一侧找这条边，假设是 $a$ 侧，也就是我们要找到 $a$ 所有边权 $\leq 2 (dist_{s, x} - dist_{s, a})$ 的出边。

那么边权 $\leq 2 (dist_{s, x} - dist_{s, a})$ 的出边多不多呢，直觉上是不多的，因为看起来就和边权 $\leq (dist_{s, x} - dist_{s, a})$ 的出边差不了两倍嘛！后者就是最短路树内部的边，根据我们之前的说法，只有 $O(\sqrt{n})$ 条，所以我们这么枚举边数肯定不多！

如果你只想感性理解，这里就结束了，时间复杂度为 $O(q\sqrt{n}\log{n} + m\log{m})$。但是严谨的来说，我们知道 $a$ 的出边边权和 $(dist_{s, x} - dist_{s, a})$ 并不独立，我们还得证明 $\leq 2 (dist_{s, x} - dist_{s, a})$ 的出边不多。

证明

定理：我们有至少 $1-O(n^{-5})$ 的概率，对于任意 $a, v$，记 $A$ 为 $a$ 出边边权 $\leq v$ 的边数，$B$ 为 $\leq 2v$ 的边数，我们有：$B < 64\log n + 4A$。

证明： 对于一对固定的 $(a, v)$，我们先掏出 $a$ 所有边权 $\leq 2v$ 的出边，一共有 $B$ 条，在这个前提下，每条边有 $\frac{1}{2}$ 的概率边权 $\leq v$，且独立。

如果 $B < 64 \log_2 n$，显然成立。不然，根据 Chernoff Bound，$Pr[A \leq \frac{B}{4}] \leq e^{-\frac{B}{8}} \leq e^{8\log_2 n} \leq n^{-8}$，也就是说几乎一定成立。

根据 Union Bound，我们可以得知，所有 $(a, v)$ 成立的概率至少有 $1 - n^{-8} \times n \times V$，至于怎么把 $V$ 去掉，我懒得写了。

这个证明多带了一个 $\log$，确实不太优美，但是并不影响时间复杂度，当然，实测一下还是比较像 $O(\sqrt{n})$ 的。