DNA 匹配
题目来源:
- 2021-2022 ICPC Asia Pacific - Yokohama Regional, Problem H
- Moscow Pre-Finals Workshops 2022 Day 4, Problem H
QOJ 链接:https://qoj.ac/contest/912/problem/3801
都 2202 年了怎么还有输出实数的非计算几何题啊?怎么相对误差在 0.05 以内都算对?
这么离谱的误差范围,不难想到这题应该想一些乱搞。
毛估估一下会发现容斥并不是个好方法。尽管取的 s_i 变多之后概率会迅速变小,但是组合数会迅速变大,所以简单地在某个大小进行截断是无法通过此题的。
另辟蹊径,注意到有一档部分分保证 ans\ge 0.01 ,所以可以用蒙特卡罗法进行随机抽样来估计概率。
蒙特卡罗法的不足之处在于,当答案太小时很难抽中一个合法的 DNA 序列,于是估计结果总是为 0 。但是我们可以限制随机抽样的范围,来保证抽中的序列总是合法的。所以可以想到,我们可以只在合法的 DNA 序列中抽样。
先设置一个贡献的分配方式。对于每一个 DNA 序列 t ,若其在所有 m 个串中可以匹配 k\ (k>0) 个,那么 t 会给每个能匹配的 s_i 带来 \frac 1 k 的贡献。
我们对每个 s_i 分别计算贡献。仍然使用蒙特卡罗法,但是显然只有能匹配 s_i 的 DNA 序列才能对 s_i 带来贡献,因此我们让抽取的 DNA 序列 t 在匹配 s_i 的序列中随机,最后再除掉匹配 s_i 的概率。这样就解决了答案太小的问题。
也可以让 t 只给第一个匹配的 s_i 带来 1 的贡献,做法是一样的。
区间数颜色
题目来源:
- Petrozavodsk Winter 2022. Day 2. KAIST Contest + KOI TST 2021, Problem H
QOJ 链接:https://qoj.ac/contest/820/problem/2559
考虑假如存在 L_j\le L_i,R_i\le R_j,i< j,那么 i 一定比 j 要早出现在答案里。
一开始,我们把区间按照左端点排序。
当一个区间包含的所有区间都已经加入答案之后,我们再把这个区间加入候选集合。一开始,我们先把不包含其他区间的区间加入候选集合。我们把候选集合里的区间按左端点排序,这样它们的编号也是有序的(事实上,你发现这样右端点也是有序的)。
考虑离散化之后,区间的端点把整个数轴划分成 O(n) 个段,我们每次把某个区间加入答案,相当于覆盖掉某些段。那么一个段被覆盖后,包含这个段的区间在候选集合里是连续的一段。
我们对于每个区间维护一个 \text{remain}_i 表示现在第 i 个区间里没被覆盖的段长之和,对于不在候选集合里的,我们认为是 +\infty。
那么就是对标号在某个区间内的 \text{remain}_i 减去这段的长度。我们可以用一个 set 维护哪些段没被覆盖,然后用一个树状数组维护一个区间内没被覆盖的段长之和,这样我们在把某个区间加入候选集合的时候也可以知道它的 \text{remain}。
考虑我们把某个区间加入答案后,我们就从候选集合删去它后,此刻可能有一些区间可以加入候选区间,那么找到候选集合里这个区间的前驱 j 和后继 k,那么可以加入的区间一定包含于 (L_j,R_k),那么我们需要它的编号比 j 大,并且右端点比 R_k 小,那么每次找到标号在 (j,n] 里的区间里右端点最小的区间尝试加入,再用一棵线段树维护即可。
复杂度 O(n\log n)。
情报传递 2
题目来源:第13回日本情報オリンピック 春季トレーニング合宿, Day 4, Task 漢字しりとり(Kanji Shiritori)
QOJ 链接:https://qoj.ac/contest/337/problem/1407
算法 1
通信题好难啊,还是弃疗吧。直接让 Spy 把 Participant 不知道的信息都发送过去咋样?
计算一下,一共需要发送 K 条边的边权,总共需要 K \cdot \left\lceil \log_2 W\right\rceil = 5 \times 54 = 270 个 bit。随后让 Participant 运行 Floyd 算法,记录过程中更新的最短路并复原该路径即可。
共需 270 个 bit,可以通过子任务 1,得到 5 分。
算法 2
注意到其实 Participant 不需要知道这些边的边权,甚至不需要知道最后最短路的长度 - 他只需要知道方案就可以了!
注意到由于所有边权未知的边的起点均相同,又有所有边权均非负,这意味着我们不可能经过一个顶点超过一次,所以我们可以将最短路分为 K+1 类:
- 第 1 \leq i \leq K 类经过了第 i 条未知边
- 第 0 类没有经过任何未知边。
注意到对于第 0 类,我们可以直接删掉所有未知边跑最短路,其余第 i 类最短路一定形如 S_j \to A_i \to B_i \to T_j 的形式,同样可以删掉所有未知边来跑。
因此,我们只需要让 Spy 预先跑出所有询问的答案,并将询问类型发送给 Participant 即可。
一共需要 Q \cdot \left\lceil \log_2 (K+1) \right\rceil = 60 \times 3 = 180 个 bit,刚好可以在子任务 2 中获得 11 分,共获得 16 分。
算法 3
注意到算法 2 中,一组询问只需要发送一个 0 \sim 5 内的数,却要使用 3 个 bit,有些愚蠢。我们可以仿照进制转换,将这个 60 位的 6 进制数直接转成 2 进制数发送过去,然后再转换回来即可。
如果懒得写高精度,也可以直接用 8 个 bit 压 3 个数(6^3 = 216 < 2^8 = 256),这样需要 20 \times 8 = 160 个 bit,在子任务 2 中获得 15 分,共获得 20 分。
如果写了高精度,那么 6^{60} = 48873677980689257489322752273774603865660850176,而注意到 2^{156} = 91343852333181432387730302044767688728495783936,因此我们只需要发送 156 个 bit,在子任务 2 中获得 17.4 分,共获得 22.4 分。
当然事实上我们可以利用长度作为信息,只发送 155 个 bit,获得额外的 0.6 分,这样就可以在子任务 2 中获得 18 分,共获得 23 分。
算法 4
我们设 f(i, a, b) 表示对于第 i 个问题,第 a 种最短路和第 b 种最短路哪个更短。
那么对于 Participant 而言,他只需要对所有 0 \leq i < Q, 0 \leq a,b \leq 5,都得到 f(i,a,b) 的值,那么问题就解决了。
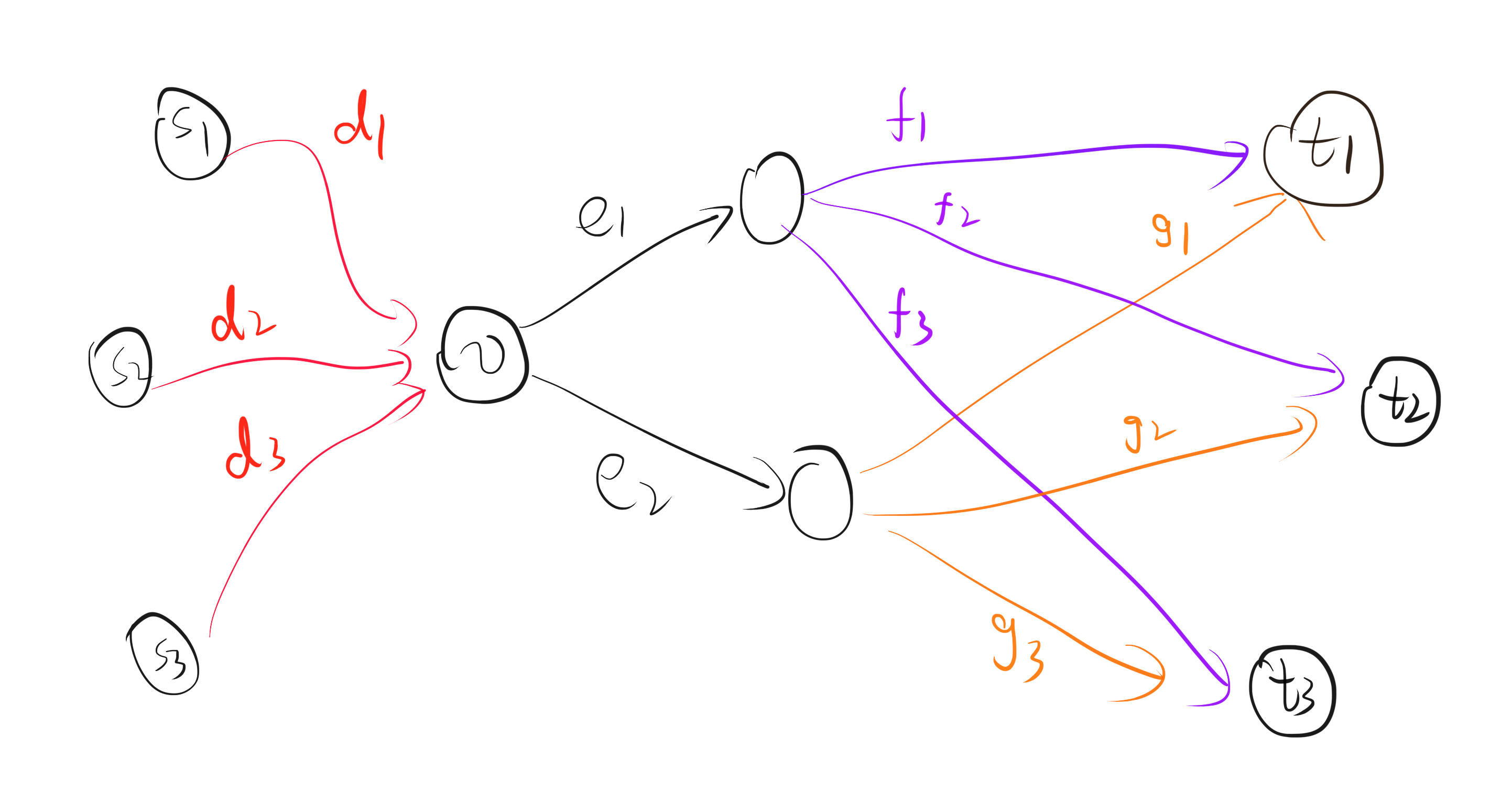
考虑对于以上三组询问中,方案 1 比方案 2 优秀,当且仅当 d_1+e_1+f_1 < d_1 + e_2 + g_1,即 e_1 - e_2 < g_1 - f_1。同理,我们可以发现,对每个 0 \leq i < Q,方案 a 比方案 b 优秀,都可以表示成不等式 e_a - e_b \leq X_{i,b}-X_{i,a} 的形式。注意到双方事实上都知道 X_{i,b} - X_{i,a} 的值,于是我们可以对所有 \binom{6}{2} = 15 种不同的 0 \leq a < b \leq K,计算出 X_{i,b} - X_{i,a} 的值并将他们排序。随后由 Spy 发送给 Participant 一个值 R_{a,b},表示从大到小 R_{a,b} 个 X_{i,b} - X_{i,a} 是能满足 e_a-e_b \leq X_{i,b}-X_{i,a} 的最后一个 i。这样我们便成功发送了 f(i,a,b) 的值。
总共有 15 个 (a,b),每个需要发送一个 0 \sim Q 内的值,共需 \frac{K(K+1)}{2} \left\lceil\log_2 (Q+1)\right\rceil = 15 \times \left\lceil \log_2 61 \right\rceil = 90 个 bit。可以在子任务 2 中获得 43 分,共获得 48 分。
当然你也可以结合算法 3 中的优化方法,61^{15} = 602486784535040403801858901 < 2^{89},因此只需要发送 88 个 bit 即可,获得额外的 0.3077 分。
算法 5
注意到算法 4 的本质即为,我们不断选取 a,b,并比较有多少组询问中 a 优于 b,基于此将所有询问分成两组。
Spy 将所有的限制均发送给了 Participant,但事实上双方可以预先商定策略,因此我们不妨固定选取 a,b,并考虑分组的过程:
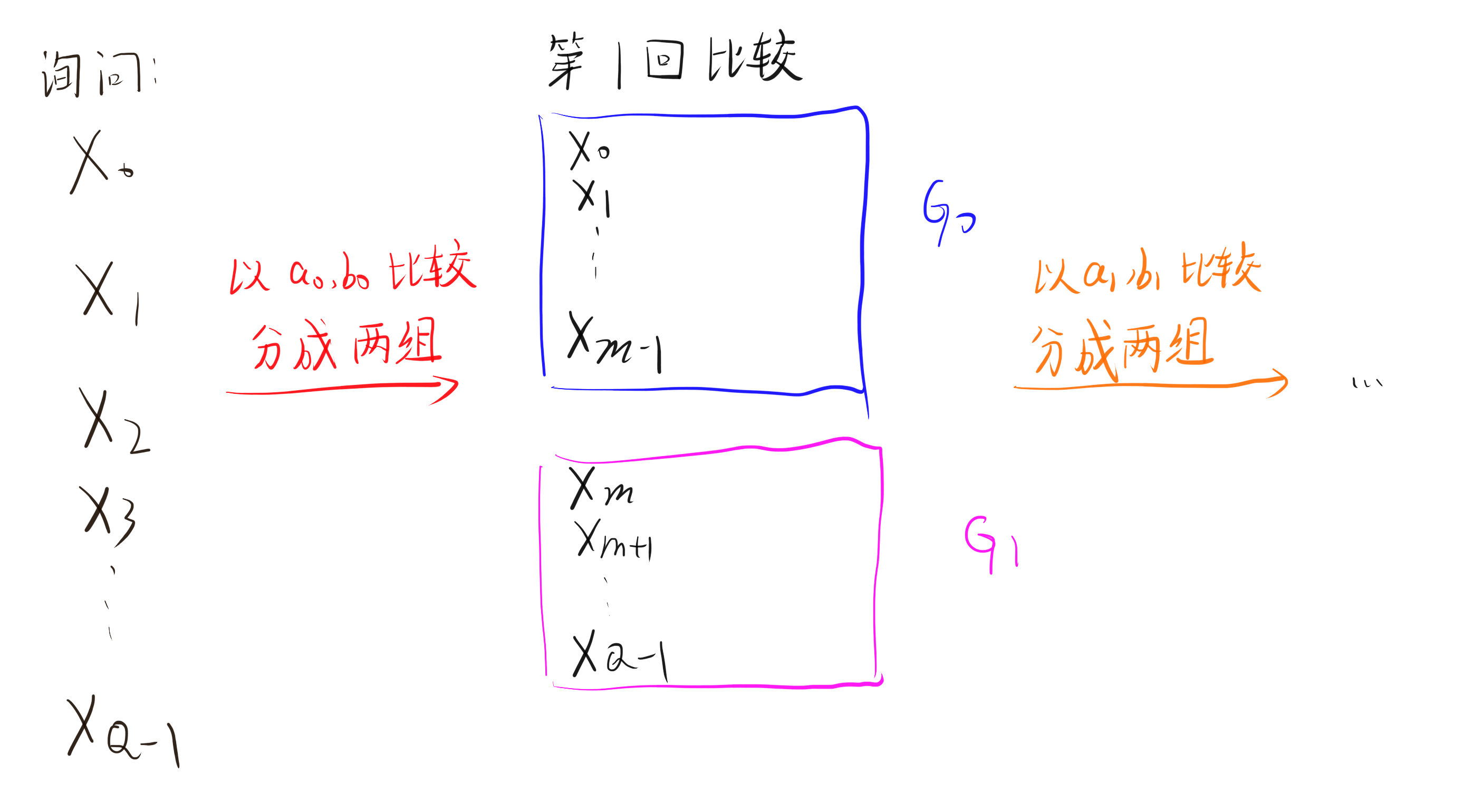
注意到对于固定的 a_i, b_i,我们发送的本质即为 m 的值。虽然参与排序的段很多,但由于 m 一定恰好落在了一组询问区间中,因此事实上,只有一组询问区间的 m 是有用的,其余的 m 并不会划分出更多的区间:
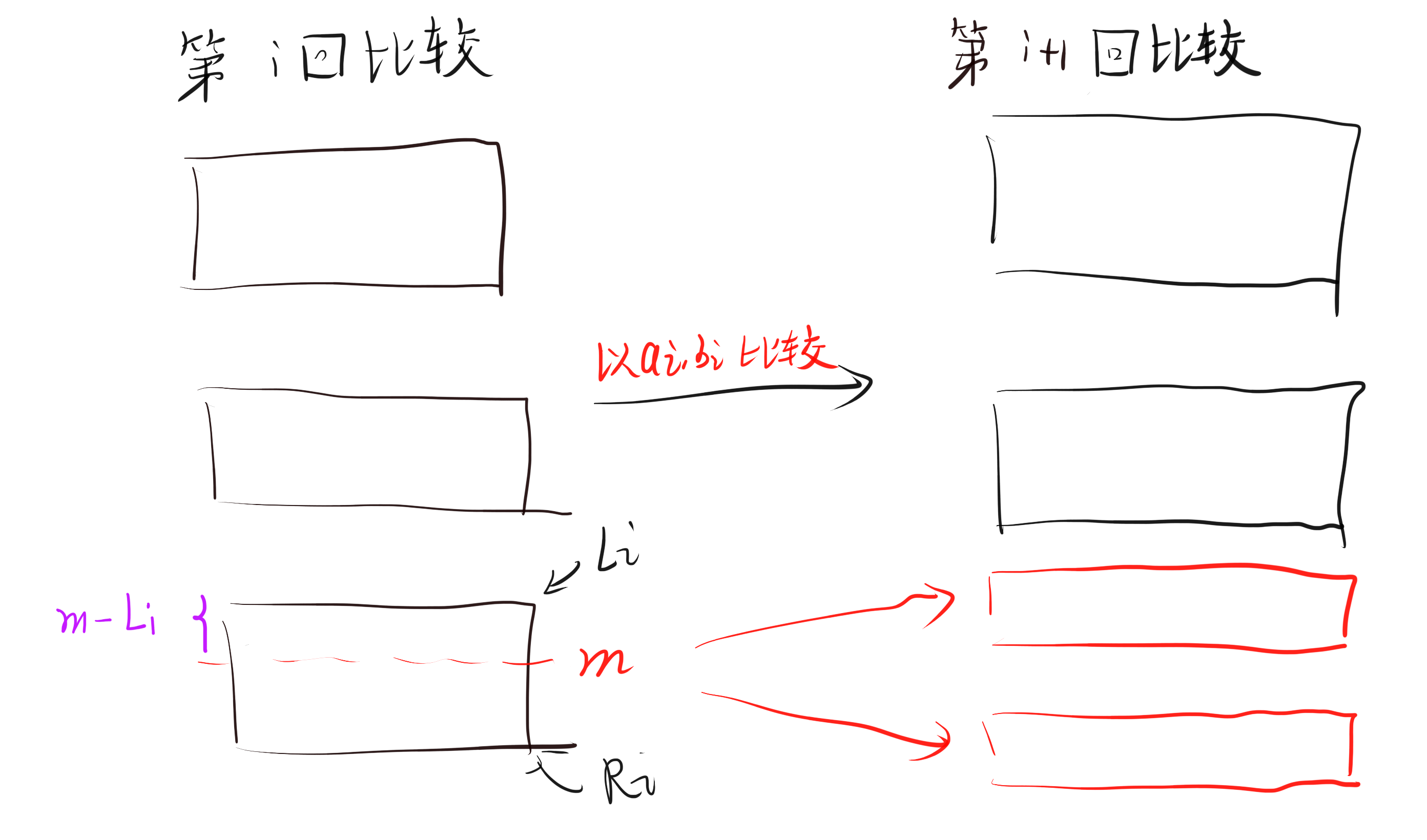
注意到我们已经预先将询问排序,因此当在进行到第 i 回比较时,在此回合参与比较的询问是一段连续的区间 [L_i, R_i],考虑不发送 m 的值,而是发送 m-L_i 的值。这样的问题是我们不知道 m 落在了哪一个区间中,因此我们考虑修改 a,b 的顺序。若干个随机算法需要发送 70 \sim 80 个 bit,可以得到 55 \sim 78 分。
不妨假设在第一回,我们进行了询问 (x, y),考虑在第二回进行 (x, z)。注意到由于我们已经确定了 x 最优的范围,因此只有 z \in [L_1, R_1] 时,m_{xz} 的值才有意义,否则一定是要么整个区间被划给了 x(等价于 x=R_1),要么是整个区间被划给了 z(等价于 x=L_0)。
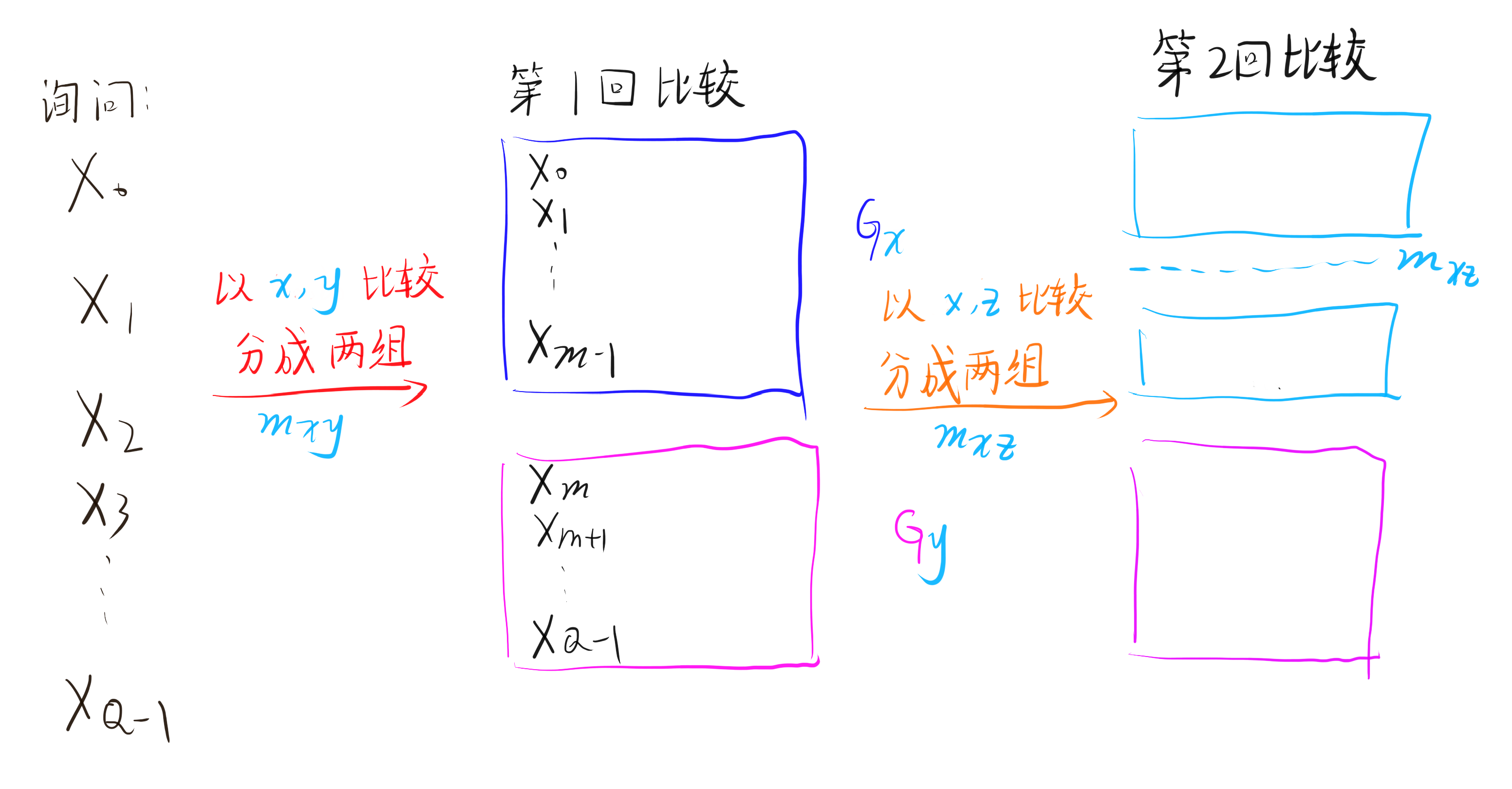
因此我们直接这样进行比较,就只需要发送 m_i-L_i 的值。
我们可以通过一边预处理到此时的 [L_i, R_i],一边计算出所需位数 d,就可以提取出接下来的 d 位用于存储 m_i-L_i。
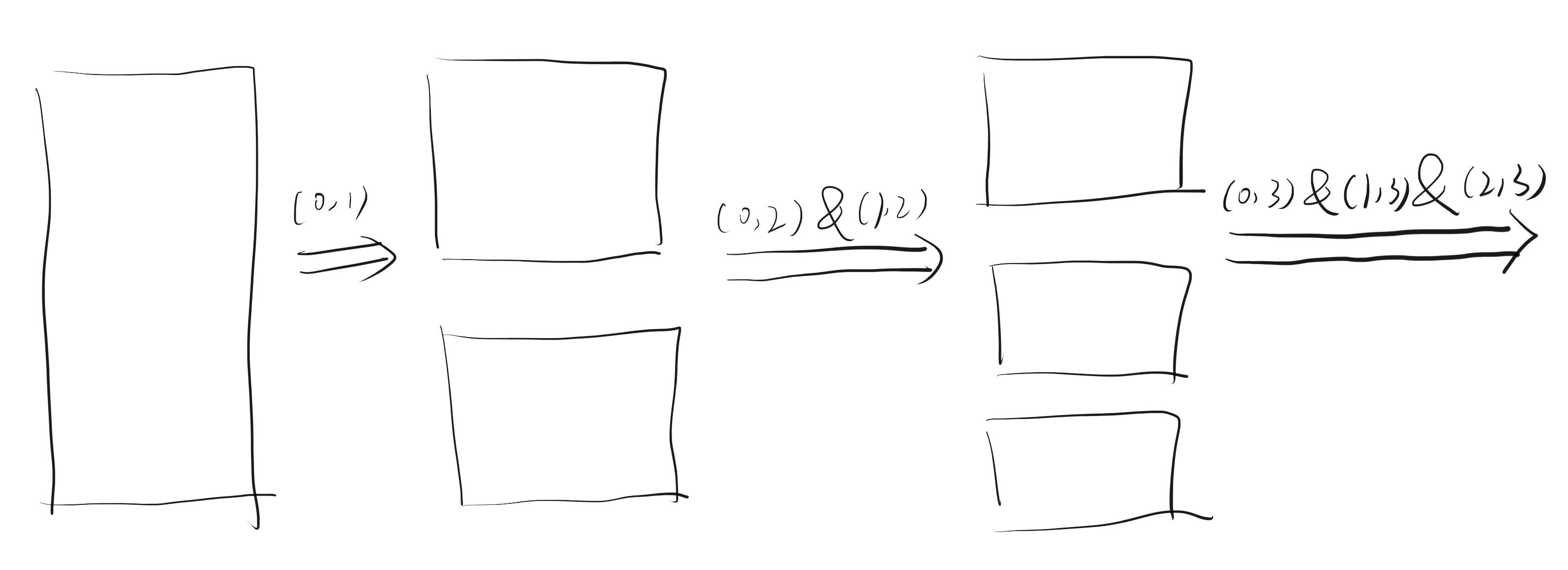
通过分析,发现当每段被划分的相等时,所需的代价最多,此时代价为:
\sum_{i=1}^{K} i\left\lceil\log_2 \frac{Q+1}{i}\right\rceil
总共需要 64 个 bit,期望得分 100 分。





