Qingyu✨ 的網誌
網誌
MIT
The 2nd Universal Cup Finals Analysis(草稿)
The 2nd Universal Cup Finals: Analysis Report
This is the draft of the problems of the 2nd Universal Cup Finals. We expect to officially release a version of this document in a few months. If you find an error, please send an e-mail to [email protected] or a private message to me (@Qingyu) about it.
The 2nd Universal Cup Finals - Schedule
Attachments
Overall Schedule
- To contestants: Please wear the blue hoodie on 19th, 21st and 23rd Feb, and the white one on 20th and 22nd Feb.
- To staff and volunteers: Please wear the red hoodie on 19th, 21st and 23rd Feb, and the green one on 20th and 22nd Feb.
| Wednesday February 19 – Registration | |||||||
| Start | End | Description | Location | Attendees | |||
|---|---|---|---|---|---|---|---|
| 13:00 | 21:00 | Check-in | Huawei Sanyapo Campus | All with badges | |||
| 18:00 | 21:00 | Team Photo | Prague Meeting Room, 3F, Building A1, Huawei Sanyapo Campus | UCup Finals Attendees | |||
| 20:00 | 20:30 | Welcome Party | |||||
| 20:30 | 22:00 | Holdem’s Night | |||||
| Thursday February 20 – City Tour | |||||||
| Start | End | Description | Location | Attendees | |||
| 08:00 | 10:00 | Breakfast | Amber Taste, The Amber House Songshan Lake Dongguan | All with badges | |||
| 10:00 | 11:00 | Transportation by bus | Hotel Lobby, The Amber House Songshan Lake Dongguan | ||||
| 11:00 | 21:00 | City Tour | Guangzhou | ||||
| Friday February 21 – Opening Ceremony / The 2025 Huawei Tech Arena Universal Cup Finals Challenge / Practice Session | |||||||
| Start | End | Description | Location | Attendees | |||
| 7:30 | 8:30 | Breakfast | Amber Taste, The Amber House Songshan Lake Dongguan | All with badges | |||
| 8:30 | 8:50 | Transportation to Xicun Campus | Hotel Lobby, The Amber House Songshan Lake Dongguan | ||||
| 08:50 | 10:30 | Opening Ceremony | Building M3, Huawei Xicun Campus | UCup Finals Attendees | |||
| 10:30 | 11:00 | Workstation Setup | |||||
| 11:00 | 16:00 | The 2025 Huawei Tech Arena Universal Cup Finals Challenge | |||||
| 16:45 | 17:45 | Practice Session | |||||
| 17:45 | 18:00 | Transportation to Sanyapo Campus | All with badges | ||||
| 18:15 | 19:30 | Dinner | Curitis Restaurant, Huawei Sanyapo Campus | ||||
| 20:30 | 22:30 | Table Tennis’ Night | Building B4, Huawei Sanyapo Campus | UCup Finals Attendees | |||
| Saturday February 22 – The 2025 Universal Cup Finals | |||||||
| Start | End | Description | Location | Attendees | |||
| 8:00 | 10:00 | Breakfast | Amber Taste, The Amber House Songshan Lake Dongguan | All with badges | |||
| 10:00 | 10:20 | Transportation to Xicun Campus | Hotel Lobby, The Amber House Songshan Lake Dongguan | ||||
| 10:30 | 16:30 | The 2025 Universal Cup Finals | Building M3, Huawei Xicun Campus | UCup Finals Attendees | |||
| 16:30 | 17:15 | Visit Tour in Xicun Campus | Huawei Xicun Campus | All with badges | |||
| 17:15 | 18:45 | Dinner | 10 Garden De Fribourg, Huawei Xicun Campus | ||||
| 18:45 | 19:00 | Transportation to Sanyapo Campus | |||||
| 20:00 | 22:30 | Video Game’s Night | Liberec Meeting Room, 2F, Building A1, Huawei Sanyapo Campus | UCup Finals Attendees | |||
| Sunday February 23 – Challenge Roadshow / The 2025 Universal Cup Conference for Competitive Programming / Closing Ceremony | |||||||
| Start | End | Description | Location | Attendees | |||
| 7:30 | 8:30 | Breakfast | Amber Taste, The Amber House Songshan Lake Dongguan | All with badges | |||
| 8:30 | 9:00 | Transportation to Xicun Campus | Hotel Lobby, The Amber House Songshan Lake Dongguan | ||||
| 09:00 | 12:00 | Challenge Roadshow | Building M3, Huawei Xicun Campus | ||||
| 12:00 | 13:00 | Lunch | KUNYU, Huawei Xicun Campus | ||||
| 13:30 | 16:35 | The 2025 Universal Cup Conference for Competitive Programming | Building M3, Huawei Xicun Campus | ||||
| 16:50 | 17:45 | Closing ceremony | |||||
| 17:45 | 18:00 | Transportation to Sanyapo Campus | |||||
| 18:30 | 20:00 | Farewell Dinner | No.1 Lake View Restaurant, Huawei Sanyapo Campus | ||||
| Monday February 24 – Checkout | |||||||
| Start | End | Description | Location | Attendees | |||
| All Day | Checkout | Huawei Sanyapo Campus | All with badges | ||||
Notice
- On February 19th, there is no group dining. You may order room service and we will cover the cost.
- For everyday’s breakfast, please use your room card to enter the dining room.
- For all transportation from Sanyapo Campus, please be at Hotel Lobby, The Amber House Songshan Lake Dongguan in time.
- If you encounter any unexpected circumstances, please contact volunteers immediately.
- To ensure the safety of all participants and the smooth operation of the event,
please strictly adhere to the on-site safety regulations.
- During the event, do not leave the designated area without permission, and refrain from climbing, chasing, using open flames, or engaging in any other behavior that may endanger yourself or others.
- All participants must follow the instructions of staff and volunteers, as well as comply with venue signage and safety notices.
- If any personal actions (such as ignoring warnings, unauthorized movement, or dangerous activities) result in personal injury, property damage, or other adverse consequences, the individual involved shall bear full responsibility for all resulting liabilities and losses.
- The event organizers will not be held accountable.
Programming Environment
- OS: Ubuntu 24.04.1 LTS
- Desktop: GNOME Flashback
- Editors: vi/vim, gvim, emacs, gedit, geany, kate
- IDEs: Eclipse, IntelliJ, CLion, PyCharm, RustRover, Code::Blocks, Visual Studio Code
- Contest Control System: DOMJudge 8.3.1
Languages
| Language | Version |
|---|---|
| C (gcc) | 13.2.0 |
| C++ (g++) | 13.2.0 |
| D (dmd) | 2.109.1 |
| Java (openjdk) | 21.0.4 |
| Kotlin (kotlinc) | 1.9.24 |
| Python (pypy3) | 7.3.15 with Python 3.9.18 |
| Rust (rustc) | 1.75.0 |
Conference Information
Linear Systems Surprises
Presenter: __Richard Peng__
Abstract: Algorithms researchers strive to design better ways of solving problems that are central to many disciplines. Systems of linear equations arise throughout engineering and sciences in tasks ranging from physical simulation to data analytics. In many cases where linear systems don’t exactly model the problem, they provide the steps that lead to the solutions. Despite linear systems’ storied history spanning centuries, the current best algorithms for general linear systems, as well as many important subclasses, remain comparatively slow.
Over the last few decades, algorithms researchers developed entirely new approaches to solving linear systems. These progress led to accelerations in many applications, as well as entirely new theoretical frameworks for designing and analyzing algorithms. This talk will briefly overview some of the surprising ways of thinking about approximations, iterative convergences, and algebraic structures that originated from studying linear systems.
An Introduction to Symbolic Program Generation
Presenter: __Ruyi Ji__
Abstract: Large Language Models (LLMs) have recently achieved remarkable success in program generation, particularly in competitive programming. For example, OpenAI reported that its o1 model achieved gold medal-level performance in last year's International Olympiad in Informatics (IOI), and its o3 model attained an estimated rating of ~2700 on Codeforces, ranking among top competitive programmers.
Despite these impressive milestones, current LLMs still suffer from several limitations. One major challenge is their inability to deduce general rules purely from examples, as their inference heavily depends on the presence of natural language. To address this limitation, symbolic approaches — representing a different paradigm of artificial intelligence — offer a complementary solution. Unlike LLMs, which rely on fitting vast amounts of data through large neural networks, symbolic systems represent knowledge via a small set of interpretable rules and perform reasoning by searching through combinations of these rules. While such systems are less effective at handling natural language, they excel at reasoning directly from structured examples.
In this presentation, I will provide an overview of symbolic program generation (i.e., program synthesis) and share recent progress in synthesizing efficient programs and complex algorithms.
Tight Bounds for Retrieval Data Structures By
Presenter: __Tingqiang Xu__
Abstract: Retrieval data structures are data structures that answer key-value queries without paying the space overhead of explicitly storing keys. The problem can be formulated in four settings (static, value-dynamic, incremental, or dynamic), each of which offers different levels of dynamism to the user. In this presentation, I will talk about optimal bounds for the final two settings (incremental and dynamic) in the case of a polynomial universe. This complete a line of work that has spanned more than two decades, and also come with a surprise: the incremental setting, which has long been viewed as essentially equivalent to the dynamic one, actually has a phase transition, in which, as the value size v approaches log n, the optimal space redundancy actually begins to shrink, going from roughly n log log n (which has long been thought to be optimal) all the way down to Θ(n) (which is the optimal bound even for the seemingly much-easier value-dynamic setting).
Practice on medical LLMs
Presenter: __Benyou Wang__
Abstract: Recently, OpenAI's ChatGPT and various open-source community models, such as LLaMA 3, have significantly advanced the development of AI applications. In the medical field, both proprietary and open-source models hold great potential. However, when it comes to solving real-world medical problems, there is still a "last mile" to cover. In this Speech, we will introduce our team's development of the medical large language model, HuatuoGPT, and its multilingual and multimodal extensions, the Apollo series. We will also discuss the technical solutions for HuatuoGPT-o1, which aim to enhance the performance and interpretability of large language models, particularly in the context of longer diagnostic reasoning chains. Finally, we will look ahead to the future development of medical LLMs. Specifically, we will explore the potential of using AIGC technology to create a large number of patient agents to train both human and AI doctors. By doing so, we can accumulate real patient needs and doctor feedback, ultimately working towards the development of generalist medical artificial intelligence (GMAI).
The 2nd Universal Cup Finals - 比赛规则
第二届 Universal Cup 总决赛规则
最后更新:2025年2月21日
Qingyu - Universal Cup 执行委员会
English Version of this document can be found here.
Universal Cup 是一个致力于服务竞赛编程社区的组织,专注于提供高质量的训练资源并举办全球线下赛事。2025 年 Universal Cup 总决赛(即第二届 Universal Cup 总决赛)是本赛事第二赛季的最终比赛。
共有 20 支队伍通过在线比赛、半决赛或线下夏季峰会晋级,将争夺第二届 Universal Cup 冠军的头衔。
竞赛形式
- 竞赛时长为五小时。在不可预见的情况下,科学委员会主席有权修改竞赛时长。如竞赛形式或时长发生变更,参赛队伍将以统一方式及时获悉。
- 竞赛题目数量不少于 10 题,且不超过 14 题。
- 队伍可通过 Clarification Request 提交对题目可能存在错误的申诉。澄清请求必须仅使用英文撰写。
- 竞赛期间可能发布 Clarification,内容可能包括题目说明、附加细节、额外示例或对题目的修改(包括补充、删除或更改)。
- 所有 Clarification 信息均仅以英文提供,并会在竞赛现场统一公布。
题目
- 所有题目陈述仅提供英文版本。
- 参赛队伍可使用字典或在线翻译工具自行翻译题目内容,官方不提供翻译。
- 任何题目均不会提供部分分数。
- 竞赛题目类型包括:
- 标准输入/输出题:程序需从 标准输入 读取数据,并将结果输出到 标准输出。
- 交互题:程序需通过标准输入/输出与 交互器 进行交互。
- 多次运行题:程序将多次运行,每次使用不同的输入数据。
- 仅输出题:参赛队伍无需提交程序,仅提交最终答案。
提交与评测
- 竞赛评测平台采用 DOMjudge,一个开源自动化竞赛系统。
- 支持的编程语言包括 C、C++、D、Python 3、Java、Kotlin 和 Rust。
- 详细的语言版本与规格请参考 TechNote 文档。
- 每次提交的评测结果仅为通过(Accepted)或未通过(Rejected),不会提供部分分数或错误测试点编号。
- 未通过的提交将标记为以下之一:
- 编译错误(CE) - 运行时错误(RTE) - 时间超限(TLE) - 结果错误(WA) - 无输出(NO) - 输出超限(OLE)
计分、排名与奖项
- 队伍按照解题数量进行排名,解出相同题目数量的队伍按照 罚时 进行排名。
- 如罚时相同,则按 最后一个通过题目的提交时间 进行排名。如果仍有相同,将按照以下方式,直到决出所有相同队伍的名次:
- 所有排名相同的队伍将按照他们的 最后一次通过提交的提交时间(精确到毫秒) 排名。该时间越早的队伍排名越高。没有通过任何题目的队伍的时间被视为
00:00:00.000 - 如果仍有相同,这些排名相同的队伍将会按照他们在第 2 届 Universal Cup 中的 rating 进行排名。
- 如果仍有相同,一道用于打破平局的额外题目将决定这些排名相同的队伍的排名。
- 如果仍有相同,将通过抽签决定这些队伍的排名。
- 所有排名相同的队伍将按照他们的 最后一次通过提交的提交时间(精确到毫秒) 排名。该时间越早的队伍排名越高。没有通过任何题目的队伍的时间被视为
- 罚时 计算方式为 所有解出的题目的耗时总和 加上 该题目的额外罚时。
- 题目的耗时是指从竞赛开始到首次通过该题的提交时间,以分钟计算。
- 题目的额外罚时为 20 分钟 乘以 首次通过前所有未通过的提交次数(编译错误除外)。
- 未解决的题目不计算罚时。
- 比赛进行 4 小时后,实时排名将被冻结,之后的提交结果将在榜单上显示为“待定”。
- 金牌将会颁发给比赛中获得前三名的队伍(共三名)。
- 银牌将会颁发给比赛中获得第四名至第七名的队伍(共四名)。
- 铜牌将会颁发给比赛中获得前八名至第十二名的队伍(共五名)。
- 科学委员会主席有权决定为队伍颁发额外的奖牌。
竞赛环境
- 每支队伍仅配备 一台计算机。
- 所有队伍的计算机配置相同。
- 队伍可自带 鼠标、键盘 或 手写板 进入比赛区域,但不保证所有外接设备都能正常使用。
- 队伍不得携带 个人计算机、手机、计算器 或其他电子设备进入比赛区域。
- 技术委员会有权检查队伍携带的外接设备。如有争议,技术委员会主席的决定为最终裁决。
- 参赛队伍可浏览互联网以获取任何资料。
- 竞赛期间,禁止与队伍以外的任何人交流。
- 任何在互联网上分发题解、代码或辅助程序的行为均被严禁。
- 参赛队伍不得提交恶意代码,包括但不限于攻击评测系统或恶意占用评测资源。
- 在科学委员会主席指示前,不得触碰比赛工作站的任何设备。
申诉
- 参赛队伍可对题目内容、提交评测结果或竞赛相关决定提出申诉。
- 申诉内容必须仅使用英文撰写。
- 评测裁判将对申诉做出决定,可能会调整竞赛期间的评测结果。
- 如果对裁判决定仍有异议,可向 Universal Cup 科学委员会主席提交最终申诉。
- 科学委员会主席的决定为最终裁决。
竞赛委员会
科学委员会
- 主席: Qingyu
- 副主席: jiangly
- 委员: bulijiojiodibuliduo, quailty, Heltion, Lynkcat
技术委员会
- 主席: Qingyu
- 委员: cubercsl, dup4, Tangent
组织委员会
- 主席: chenjb
The 2nd Universal Cup Finals - Competition Rules
The 2nd Universal Cup Finals Rules
Last update: Feb 21, 2025
The Universal Cup Executive Committee
本文档的中文版本可以在这里查看。
The Universal Cup is an organization aiming at serving the competitive programming community, dedicated to provide high quality training resources and host onsite global events. The 2025 Universal Cup Final Contest (or The 2nd Universal Cup Finals) is the final contest of the 2nd season of our event.
A total of 20 teams have qualified through online competitions, semifinals, or onsite summer summits to compete for the title of The 2nd Universal Cup Champion.
Contest Format
- The competition will last five hours. The Chair of the Scientific Committee has the authority to modify the contest duration in the event of unforeseen circumstances. If any changes occur regarding the contest format or duration, participants will be notified in a timely and uniform manner.
- There will be at least ten (10), but no more than fourteen (14) problems in the contest.
- Teams may submit claims regarding potential mistakes in a problem via a clarification request. Clarification requests must be written in English only.
- Clarifications may be issued during the competition. These clarifications may include explanations of problem statements, additional details, extra examples, or modifications to a problem (including additions, removals, or changes).
- All clarifications will be provided in English only, and notifications will be announced at the competition venue.
Problems
- All problem statements will be provided in English only.
- Teams may use dictionaries or online translation tools to translate the statements into other languages. No official translations will be provided.
- No partial scores will be awarded for any problem.
- The types of problems in the competition include:
- Standard I/O problem: Your program must read input from the standard input and write output to the standard output.
- Interactive problem: The program interacts with an interactor through standard I/O.
- Multiple-Run Problem: The program will be executed multiple times, each with a different input.
- Output-Only Problem: Teams do not submit a program but instead submit the final answers directly.
Submissions
- The judging platform of the competition is DOMjudge, an open-source automated system to run programming contests.
- The supported programming languages include C, C++, D, Python 3, Java, Kotlin, and Rust.
- The detailed language specifications should be referred to in the TechNote document.
- Each submission is judged as accepted or rejected. No partial scores or failed test ID will be given to the teams.
- Rejected runs will be marked with one of the following:
- Compilation Error (CE)
- Runtime Error (RTE)
- Time Limit Exceeded (TLE)
- Wrong Answer (WA)
- No Output (NO)
- Output Limit Exceeded (OLE)
Scoring, Ranking, and Awarding
- Teams are ranked according to the most problems solved.
- Teams who solve the same number of problems are ranked first by the least penalty, with the following tie-breakers in order:
- the tied teams will be ranked according to their last AC time, in milliseconds. Teams has the earlier last AC time will be ranked higher. Teams did not solve any problems will have the last AC time as
00:00:00.000. - if there is still a tie, the tied teams will be ranked according to their ratings on The 2nd Universal Cup.
- if there is still a tie, the tied teams will be ranked according to an additional play-off task.
- if there is still a tie, a lucky draw will determine the ranking of all tied teams.
- the tied teams will be ranked according to their last AC time, in milliseconds. Teams has the earlier last AC time will be ranked higher. Teams did not solve any problems will have the last AC time as
- The penalty is the sum of the time consumed for each problem solved plus the penalty in that problem.
- The time consumed for a solved problem is the time elapsed from the beginning of the contest to the submission of the first accepted submission, in minutes.
- The penalty in a problem is twenty (20) minutes times the number of non-accepted submissions before the first accepted submission, excluding the ones with a compilation error verdict.
- There is no time consumed for a problem that is not solved.
- The leaderboard will be frozen 4 hours after the contest starts, and the results submitted after 4 hours will be shown as pending on the leaderboard.
- Gold Medals will be awarded to the Top 3 teams (1st, 2nd, and 3rd places).
- Silver Medals will be awarded to the Next 4 teams (4th to 7th places).
- Bronze Medals will be awarded to the Next 5 teams (8th to 12th places).
- Additional Medals might be awarded at the decision of Chair of the Scientific Committee.
Contest Environment
- Each team will be provided with one computer only.
- All teams will have equivalent computing equipment.
- Teams may bring their own mouse, keyboard, or graphics tablet to the contest area. However, it is not guaranteed that all the external devices could work properly on your workstation.
- Teams may not bring their own computers, smartphones, calculators, or other electronic devices to the contest area.
- The Technical Committee may inspect the external devices brought by a team before the contest. In case of ambiguity, the decision of the Chair of the Technical Committee shall be final.
- Teams are allowed to browse the Internet to access any materials.
- Teams are prohibited from communicating with anyone outside their team during the contest.
- The distribution of any problem-solving materials, including ideas, codes, or auxiliary programs, on the Internet is strictly forbidden.
- Teams may not submit malicious codes, including but not limited to attacks on the judging platform and malicious occupation of evaluation system resources.
- Do not touch anything at the team workstations until so directed by the Chair of the Scientific Committee.
Appeal
- Teams may submit an appeal regarding potential mistakes in any problems, verdicts of the submissions, or other contest decisions.
- Appeals must be written in English only.
- Judges will give a decision to an appeal, which might change a verdict given during the contest.
- If you are still not satisfied with the results given by the judges, you may file a final appeal with the Universal Cup Scientific Committee.
- The decision of the Chair of the Scientific Committee shall be final.
Competition Staff
Scientific Committee:
- Chair: Qingyu
- Deputy Chair: jiangly
- Members: bulijiojiodibuliduo, quailty, Heltion, Lynkcat
Technical Committee:
- Chair: Qingyu
- Members: cubercsl, dup4, Tangent
Organizing Committee:
- Chair: chenjb
The 3rd Universal Cup. Stage 28: Haidian Huangzhuang 题解
A. 铁甲战士
除了最开始,抽牌堆里至少包含一张牌,也就是刚打出的那张。下面默认抽牌堆里已经包含一张牌。可以发现,如果在出剑柄打击后不出耸肩无视,那么后面迟早会把手牌全部出完,无法持久地打下去,所以剑柄打击后必须出耸肩无视。同理,如果出了一张狂怒/全身撞击,那么下一张必须要打剑柄打击。因此除了游戏开头,一定是狂怒/全身撞击,剑柄打击,耸肩无视循环出。对于游戏开头和结尾只有 $O(1)$ 种可能,可以直接枚举。可以发现,一定是一个前缀打狂怒,一个后缀打剑柄打击,直接二分分界点即可。需要写高精度。
B. 小青鱼
如果每次操作是操作一整行/列/对角线,那么题目等价于 3sum 问题,可以用一次 FFT 解决。
那么现在区间怎么做。考虑分块。把 $n\times n$ 分成 $n/B\times n/B$ 个 $B\times B$ 的块。这样每一条线会经过 $O(n/B)$ 个整块和 $O(B)$ 个散点。整块同样 FFT。散点暴力加入。复杂度 $O(n\sqrt{n\log n})$。
不想要这个 $\log n$ 因子。可以发现行的多项式的点值可以在横着扫时保留。每次更新一个单点系数可以 $O(B)$ 改完点值。对列和斜同理。这样 $\log n$ 就没了。复杂度 $O(n\sqrt n)$。
C. 货币
相当于对每个 $i$,我们需要在 $(1,i)$ 到 $(1,i+1)$ 与 $(2,i)$ 到 $(2,i+1)$ 之间选择一个走。选每一种需要一个代价,如果 $i$ 和 $i+1$ 选择了不同的行,那么就需要额外付出 $(1,i+1)$ 到 $(2,i+1)$ 之间边的代价。再加上 $m$ 条限制,是一个小型的切糕模型,直接建图跑网络流即可。
D. 广为人知题 2
本题为 IDM Problem 的 CountDistinct 查询。详细做法见 Nearly Optimal Internal Dictionary Matching。
给所有串赋一个权值 $v_t$,其中 $t$ 为一个 $s$ 的子串,初始均为 $0$。我们直接将所有模式串对应的 $v_t$ 加 $1$,查询的答案即为查询串 $s[l,r]$ 所有本质不同子串中 $v$ 的和。
考虑所有串形成的 trie(这里 trie 字符着加,为了匹配正串 SAM)。记 $f_u$ 为 $u$ 到根的所有串的 $v$ 之和。答案为 trie 上所有是 $s[l,r]$ 子串的点的 $v$ 之和。显然构成一个 trie 上包含根的连通块,答案即为:
$$\sum\limits_{u是叶子}f_u-\sum\limits_u (u儿子个数-1)f_u$$
首先考虑后者。按 $r$ 扫描线,考虑 LCT,维护 SAM 上连续上一次出现位置相同的节点。每次 access 时遇到一个连续段时,考虑段尾的点何时儿子个数 +1,应为 $l\leq \mathrm{last}-\mathrm{len}$ 且 $s[1,r]$ 所在子树第一次出现节点(即上一个连续段中的 $\mathrm{last}$ 不会在这里贡献)。所以对 $l$ 是一个区间加。查询即为单点查询。该部分时间复杂度 $O(n\log^2n+q\log n)$。
再考虑前者。首先叶子一定左端点为 $l$。其次若 $s[l,t]$ 非叶子,说明存在 $s[l',r']=s[l,t]$ 且 $t
最后考虑如何求出 $\sum\limits_{i=x}^r f_{s[l,i]}$。差分后变为若干个 $\sum\limits_{i=l}^r f_{s[l,i]}$。而这等价于广为人知题查询(IDM Problem 的 Count 查询),可以用基本子串结构(见 Nearly Optimal Internal Dictionary Matching)在 $O((n+q)\log n)$ 内解决。
总时间复杂度为 $O(n\log^2 n+q\log n)$。若 $n,q$ 同阶,可优化至 $O\left(\frac{n\log^2n}{\log\log n}\right)$。
E. 浅斟低唱
考虑维护长度 $\geq 2$ 的所有 0 的连续段和 1 的连续段,每次 1 操作是让所有 0 连续段左移一位,所有 1 连续段右移一位,2 操作同理。
例子:经过 1 操作后,
01010000111101010001110111100010101 变成
10100001011110100010111011100101010
唯一出现问题的可能即为存在一个 0 连续段与一个 1 连续段撞上了。此时可以暴力修改,由于所有连续段长度总和这时会减 2,且长度总和初始最多为 $n$,修改最多增加在每次操作的边界 ,所以总暴力修改次数为线性。
总时间复杂度为 $O((n+q)\log n)$。
F. Trash Problem
枚举左边界。此时从左往右扫,记录每个格子当前是一个 $2\times 2$ 的一半还是已经完成。每次扫的时候如果当前是一半但是下一个是黑格,那么包含这一行的就全不合法。否则如果当前是白格,就将这个状态异或 $1$。扫到某个时刻,一个区间合法当且仅当当前这些状态都是已完成,且这个区间不包含前面所说的那些行,且与所有出现过的连续状态 $1$ 的区间交的长度为偶数。前两个条件容易满足,重点在于第三个条件。
可以发现,$[l,r]$ 与所有连续状态 $1$ 的区间交的长度为偶数等价于 $[1,r]$ 与所有连续状态 $1$ 的区间交的长度为奇数的区间左端点集合等于 $[1,l-1]$ 与所有连续状态为 $1$ 的区间交的长度为奇数的区间左端点集合相同。直接扫描线扫 $r$,哈希一下,如果哈希表 $O(1)$ 复杂度即为 $O(n^3)$。
G. 分析
注意到代价为 $A$ 的操作可以直接视为加了一条重边,所以我们可以先执行所有代价为 $A$ 的操作,在考虑怎么走。可以发现加完边之后需要执行的 $B$ 操作次数即为度数为奇数的点数除以 $2$ 再 $-1$(如果没有度数为奇数的点即为 $0$)。
树形 dp,过程中考虑是否加重边,状态内记子树根的度数奇偶性和是否有度数为奇数的点即可。
时间复杂度 $O(n)$。
H. 代数
题解
首先把子树大小的 $k$ 次方改为选 $k$ 个点都在子树内的方案数。进一步,可以看作有 $n+1,n+2,\dots,n+k$ 这 $k$ 个点,每个点随机选择 $1,2,\dots,n$ 中的一个点作为父亲,问有多少种方案使得它们都在 $u$ 子树内。
考虑从前往后 dp,设 $d[i][j]$ 表示前面 $i$ 个点考虑完,有 $j$ 个点还存在没出现的儿子的子树里有 $n+1,\dots,n+k$ 这 $k$ 个点之一。那么转移即为:
- 新出现的点子树里没有 $n+1,\dots,n+k$ 这 $k$ 个点之一。那么随便接到任意一个点上即可。
- 新出现的点子树里有这 $k$ 个点之一,假设接到了点 $u$ 下面,此时 $u$ 还有别的没出现的儿子的子树里有这 $k$ 个点之一。
- 新出现的点子树里有这 $k$ 个点之一,假设接到了点 $u$ 下面,使得 $u$ 没有没出现的儿子的子树里有这 $k$ 个点之一。
要计算每个点的答案,需要从前往后做一遍,转置之后从后往前再做一遍,最后在中间统计答案即可。
时间复杂度 $O(nk)$。
I. 二十二
首先忽略所有没有用的操作。其次,全局取 min 操作一定是从小到大操作的,因为如果有两个前面大右边小,前面的一定没用,可以把它放到紧挨着小的的右边,也没用。这样每一个 max 操作就可以放在任何一个 min 操作前面,可以看作对(这个 min 对应的 $c$ 或者原本的 $c$)取 max。
所以结论即为把所有区间 max 操作的 $c$ 变为所有比 $c$ 小的 min 操作的值之一或者不变后,先操作最小的全局 min,后操作所有 max 操作,有多少种最终序列。可以区间 dp,dp 数组类似 $dp(l,r,x)$,表示区间 $[l,r]$ 内最终序列的所有数均 $\geq x$ 且 $l-1,r+1$ 两个位置 $< x$ 的方案数。因为这样只需考虑被 $[l,r]$ 包含的 max 操作。每次枚举区间最小值转移即可,会有亿点细节。
在 $n,m,k$ 同阶时,时间复杂度为 $O(n^4)$。
J. 我以渺小爱你
条件等价于把每条 hyperedge $(x,y,z)$ 拆成三条边 $(x,y),(y,z),(z,x)$ 后建成的无向图中不包含四元环。
首先构造图 $\mathrm{ER}_q$:
点:$\bmod q$ 意义下三维空间的所有不同直线。
边:两条直线垂直。
容易证明 $\mathrm{ER}_q$ 有点数 $q^2+q+1$,边数 $\frac 12 q(q+1)^2$,且图中不存在四元环。
构造答案:hyperedge 为 $\mathrm{ER}_q$ 中所有的三角形。容易验证满足边数条件。
K. 应氏杯
在钦定一个点是极小值之后,它和周围点之间的大小关系就确定了。
一个经典结论:对于一个森林,如果所有父亲小于儿子,那么赋一个排列的方案数为 $n! \prod_u \frac 1{siz_u}$。
考虑树形 dp,记 $d[u][i][j]$ 为 $u$ 子树内,钦定了 $i$ 个点为极小值,当前小于关系构成的子树大小为 $j$ 的方案数。每次钦定一个点为极小值时,它小于所有儿子,且小于它的父亲。小于它的父亲可以通过容斥变为无限制减去父亲小于它。
是一个二维背包。把一维改成维护点值+插值之后,可以做到 $O(n^3)$。
The second round of Decisions for the 2025 Universal Cup Finals proposals has been announced
In the previous two rounds of decisions, we received 45 problems from 22 problem authors. Problem authors who submitted problems can check their review status at https://qoj.ac/proposals.
The Universal Cup Finals is still accepting problem proposals! We will provide CN¥2,500 (or US$300) for each accepted problem. Even if the problem is not selected, there is a chance to receive a small gift from the committee! Problems of any difficulty and style are welcome! Interested users are welcome to contact [email protected] to submit problems. The deadline of submitting tasks is Feb 7, 2025.
IOI 2025 China Team Selection Statistics & Prediction by Qingyu
现在用户主页会显示 List of Authored Problems
现在,每个用户的主页会显示所有由本人命制的题目。
QOJ 会在每道题目的题面开头显示这道题目的作者(如果有多个,则会按照字典序显示所有作者),作为对命题人的致谢。由于该列表为手动更新,如果你希望出现在你命制的题目的题面中,请联系我将你添加到对应的页面。
花言花语
2024 年 9 月 5 日更新:
这篇文章发出来后,引起了一些激烈的讨论,也有很多来自竞赛圈子内的家长、教练,以及一些非竞赛圈子内的朋友的阅读。无论你对我或是对花子持有什么态度,我很感谢大家能花费自己宝贵的时间来阅读我这篇充满个人情绪的拙作。
有许许多多我的朋友以及陌生人在我发出这篇文章后向我表示了支持,也有很多花子的朋友向我表示震惊,很难相信花子是这样的一个人。每个人为人处事的态度都是复杂的,无论花子对别人的态度与处事风格如何,我只能分享出我在过去几年与他交往的真实记录。
当然,也有一些不了解我的网友们质疑我的动机,甚至认为我在 IOI 赛前发出这样的博客,影响到中国队的成绩,是一种对集体荣誉不负责任的小人表现。此时此刻,我就坐在 IOI 2024 Day 2 的赛场旁,看着这些选手参加第二试的比赛。从 2022 年开始,IOI 中国国家队的训练工作,每年都有找到我进行帮忙。无论是在 2023 年国家队集训的选题与评测,还是在今年直接提供了平台进行训练,在哪怕我和一位国家队队员有私人恩怨的情况下,我也对这届国家队提供了我力所能及的帮助。这届国家队的每一轮训练,我都有所参与来提供技术支持。除了没有直接选择训练题目外(我在去年参与负责了训练试题的选择,而今年则仅仅提供了技术支持),我对这届 CHN 的支持丝毫没有因为这个人的存在而受到影响,请大家来评判,到底是谁的行为是在道德败坏,是在置集体荣誉如不顾。
- 这些文字写在 9 月 4 日。由于此时我正在参加 IOI 2024 第二试选题大会,因此在第二试比赛开始后我才将这些文字公布出来。
I know this post won't add much value to the community. These stories might already be well-known in some parts of the Chinese CP community, but I always believed that it's not ideal to share the darker aspects and troubling history of someone who was once my best friend — and indeed, I tried my best to forget the existance of such people.
However, after a year filled with depression, suffering, anger, and inner turmoil, my emotions were ultimately ignited by a comment. Yeah. I can no longer suppress my feelings, and I feel so compelled to share my thoughts, even if they might come across as a bit of a rant.
引子
今天是 IOI 2024 的第一个比赛日。在比赛期间,我在 UOJ 群内对中国国家队队员黄洛天(flower,MagicalFlower)的一些评价引来了一些网友的不解。
在我与这位同学的关系彻底爆了以后,很多网友们在私下里或公屏上都对我与他发生了什么事情感到好奇,而我则基本只对自己比较熟悉的网友们讲解了事情发生的经过。半年都过去了,不少人问我为什么不把他的所作所为公之于众,让大伙们看看这位光鲜亮丽的国家队员,是怎么在对待他亲口所说“最好的朋友”与“对我的 OI 帮助最大的人”。我当时没有这么做的原因非常简单 —— 当事人在其处于风口浪尖的那个下午,向我做出了承诺,让我请求我的朋友们不要将他的所作所为公之于众。
六个月过去了,也许是我的这位好朋友承诺的作品注入了过于真切的情感,以至于半年的时间都无法让其完成。因此,不如由我来亲自帮他回顾回顾,我与他到底都有哪些故事。
故事的起点
我与花子的相识起源于 2022 年的年初。在那时,其在 UOJ 群内询问有关 Petrozavodsk Programming Camp 的信息。作为可能是近几年与 PtzCamp 接触最多的几个人之一,我对国内还有其他的高中生对如何参加毛营感兴趣感到无比的惊讶。在第一次聊天中,我便向其介绍了作为当年算法竞赛头号强国,俄罗斯的各大派系的 Camp 以及其年度活动 Open Cup 的相关信息。
很快,我们成为了无话不谈的挚友 —— 也许不仅仅是挚友。凭借我对算法竞赛训练资源的理解,我甚至成为了他算法竞赛的教练。在他高一省选前,省选失利后返校期间,以及整个暑假训练的过程中,我都付出了我的全部来帮助他。
为什么我会这么做呢?老实说,我并不知道。也许我当时并没有什么朋友,因此我希望付出一切来维护这个我仅有的朋友的友谊。此外,我确实对哪怕是陌生人也抱有强烈的善意,希望我能发挥出自己的价值。这也是我在未来几年持续运行小青鱼训练中心(2023, 2024)的核心原因 —— 既然算法竞赛训练是我为数不多具有深刻理解的 area,那我就以此创造一些自己的价值吧。
从每日在各种来源为他准备的题单(Open Cup/PA/PtzCamp/MWCamp/...),从各种渠道(在此具体列举就不太合适了)为搞来的模拟赛,以及与他一起进行的个人与组队训练(1, 2, 3, 4, 5,... 怎么搞了这么多不同的号,都记不全了),包括为他单独搞来的 opentrains、Open Cup、Bytedance Camp、Moscow-Workshops 的账号(对这些资源熟悉的同学自然十分清楚这些资源的含金量如何)…… 如果我要详细讲出我为他做出的贡献有多少,作用有多大,可能又是一篇长文才能讲清楚的内容(“深度揭秘小青鱼训练中心”)。因此,我不妨在此直接引用其在删完我好友后亲自做出的评价。
可以说,我为这位好朋友倾注了无限的情感,甚至产生了感情寄托 —— 无论是语音通话,还是文字交流,彼时的小青鱼几乎所有的时间都在与花子聊天。他成为了 QOJ 除我外唯一的管理员(https://web.archive.org/web/20221203224544/qoj.ac/user/profile/flower ),我们也相约一起为下一年的 ptzcamp 准备了一场比赛(这也成为了后来的 Qingyu, flower, and their friends' Contest)。除此以外,而我也在生活的各种方面试图对他提供一些帮助。举一个小例子,其在暑假集训期间问我能否给他点外卖,于是便有了以下几段记录。
也就在此时,我和高一的花子定下了约定,那就是双方如果进入了集训队,便一起去 PKU,未来成为 XCPC 的队友。
黑化
随着我与花子关系越来越发展,花子这个人也逐渐变得越来越黑化。在这里我不做任何评价,单纯复述几件这个时期发生的事情。
(1) THUPC 组队
简单来说,He_Ren 曾询问我是否要一起组队参加 THUPC。当时,我跟核仁说,我提前说好了要跟花花组队,所以如果要一起的话就要带个花花。核仁当时觉得我与花子的水平都不够高,不想要同时和我们两个人一起组,因此我便拒绝了整个请求,不了了之了。
随后,我把这件事情告诉了花子,过了几天,我发现花子抛弃了我加入了这支队伍,成为了新的 THUPC 代表队。整件事情过于痛苦以至于我不想再回忆起任何相关的事情,因此我只把相关的聊天记录置于此供大家欣赏。
在 CTS 2024 时,时隔一年我又在重庆向核仁提起了此事。核仁表示既然是花子当时主动找的他,他就以为他与我以某种原因商议退队了,才接受了与花子一起参赛。整个故事现在看来,我只感觉无比的色情。
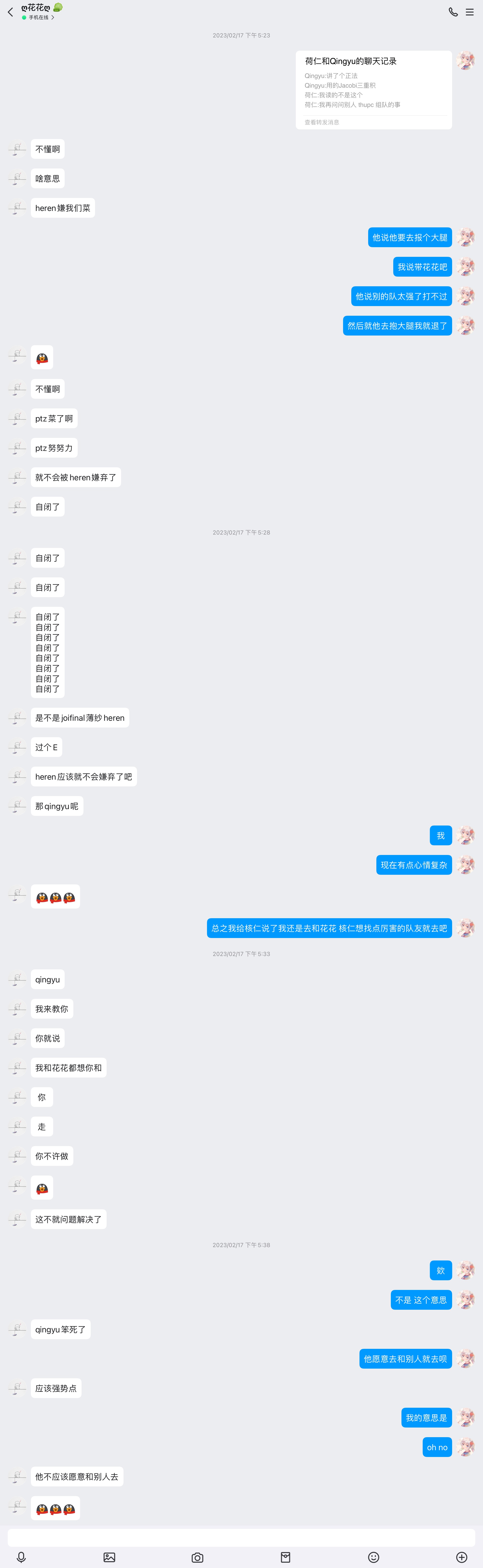
这件事情让我感到无比难受,但我当时只是认为花子觉得我水平不行才故意警告了我,没有觉得这个人的人品有什么问题。
(2) Universal Cup
在俄罗斯与乌克兰之间的冲突开始后,毛子的年度活动 Open Cup 便陷入了停滞之中。在 2023 年 2 月,我与陈靖邦 Co-Founded 了 Universal Cup。我自然也把我一切的想法都告诉了被我当做最好的朋友的花子。花子坚持想要来管理 UCup,加入组委会。由于 Committee 内我需要考虑到每个人的身份,我便对花花直言 “我可以把你拉进去,但是像cjb和杜老师可能会对你的加入存在意见”。于是,便得到了下面这一段名场面发言。
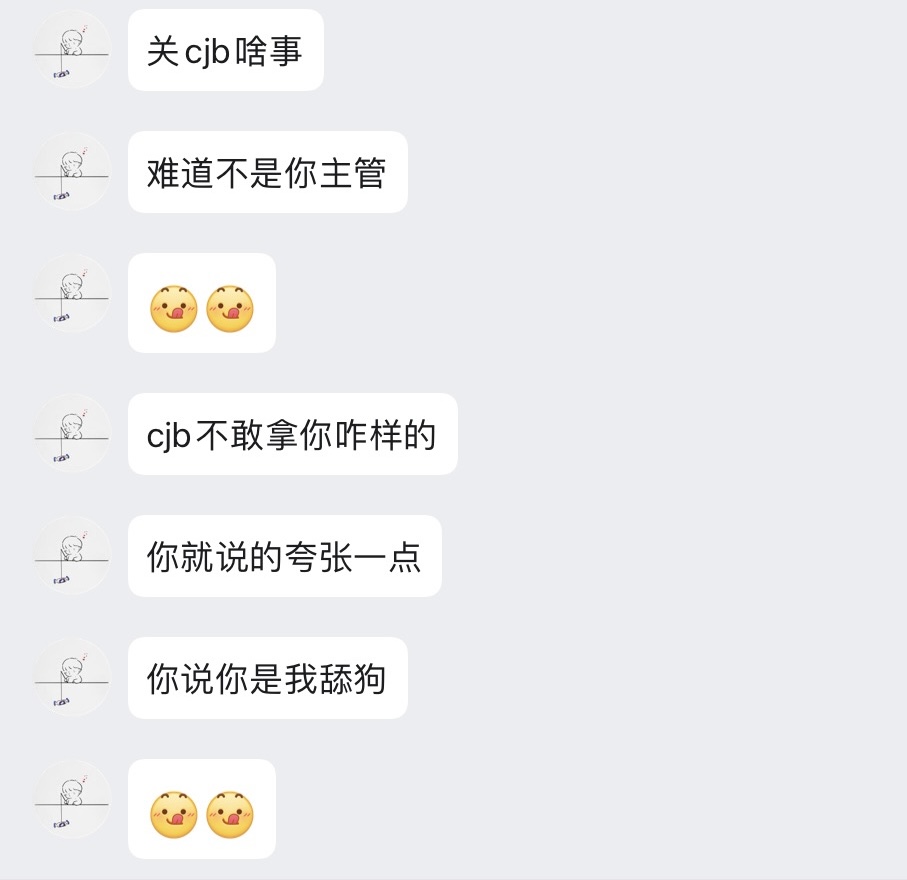
当然,在我看来,相比起后来其针对 ucup 与我本人的人身攻击而言,这个时期的花子仍然是以一种相对正常的方式与人类进行的交流。
(3) QOJ 管理员
2023年,在花子参加位于潍坊的国家队集训(注意是2023年)时,刚好他会在潍坊过生日。当时,花子告诉了我这件事情,我便询问花子我是否可以前往为他庆生。在得到了肯定的答复后,我与潍坊一中的冷老师进行了联系,并携带着送给他的生日礼物来到了潍坊一中。
结果,在我的礼物被收下后,我被冷暴力了整整一天。我完全不能理解花子是以一种什么样的心理状态,认为我总是试图与他说话让他感到很烦,因此刻意选择不与我说话。
- 什么?我怎么知道这是刻意的?在下文我会提到,花子在我与他关系第一次爆完后,是如何亲口承认这一点的。
这一次的经历让我不解。原本我向核仁说我会在潍坊待若干天,最后我一天也没有多留,当天晚上就决定离开这个不欢迎我的到来的人。我仍然无法理解为什么我们的关系成了这个样子,在未来的几天多次试图与花子交涉,问问他到底是对我有什么意见。然而,每次与花子的质问,我都没有得到他的任何理解。花子认为我对他诸如 “能不能不要总是不理我”、“为什么你不回我消息”、“为什么线下我去找你你都不搭理我的问题” 是过分的请求/亲密关系,而他不想对我这样做。
我对花子这种态度感到非常的难受,我迫切想要知道他到底是一种怎样的精神状态。而恰巧我也知道,当时他使用 QOJ 的管理权限看代码下数据的事情。在有一天,我发现花子把他向我索要 qoj 管理员时设置的 qingyutietie 的 motto 移除了。我感到是时候要问个明白了。于是在那天的中午,我撤了花子的管理权限,要求他与我对话。
那么,亲爱的花子,做出了如下的反应。
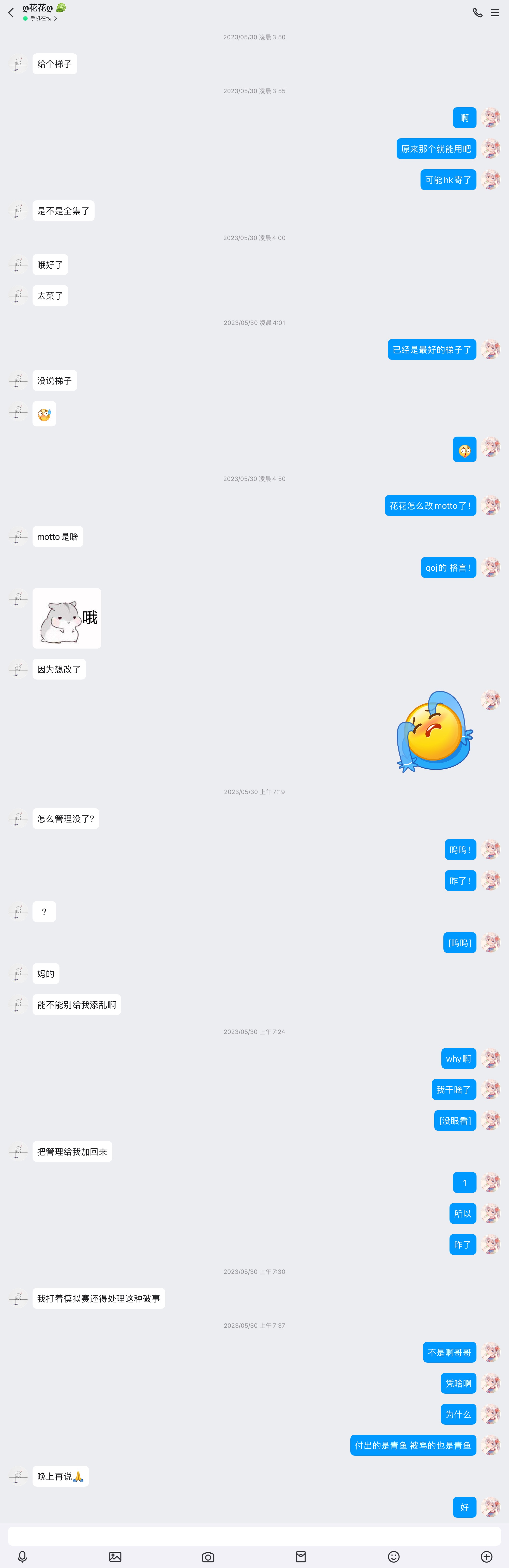
至于他说的 “晚上再说”,我也全文把我们晚上的谈话刊载出来。
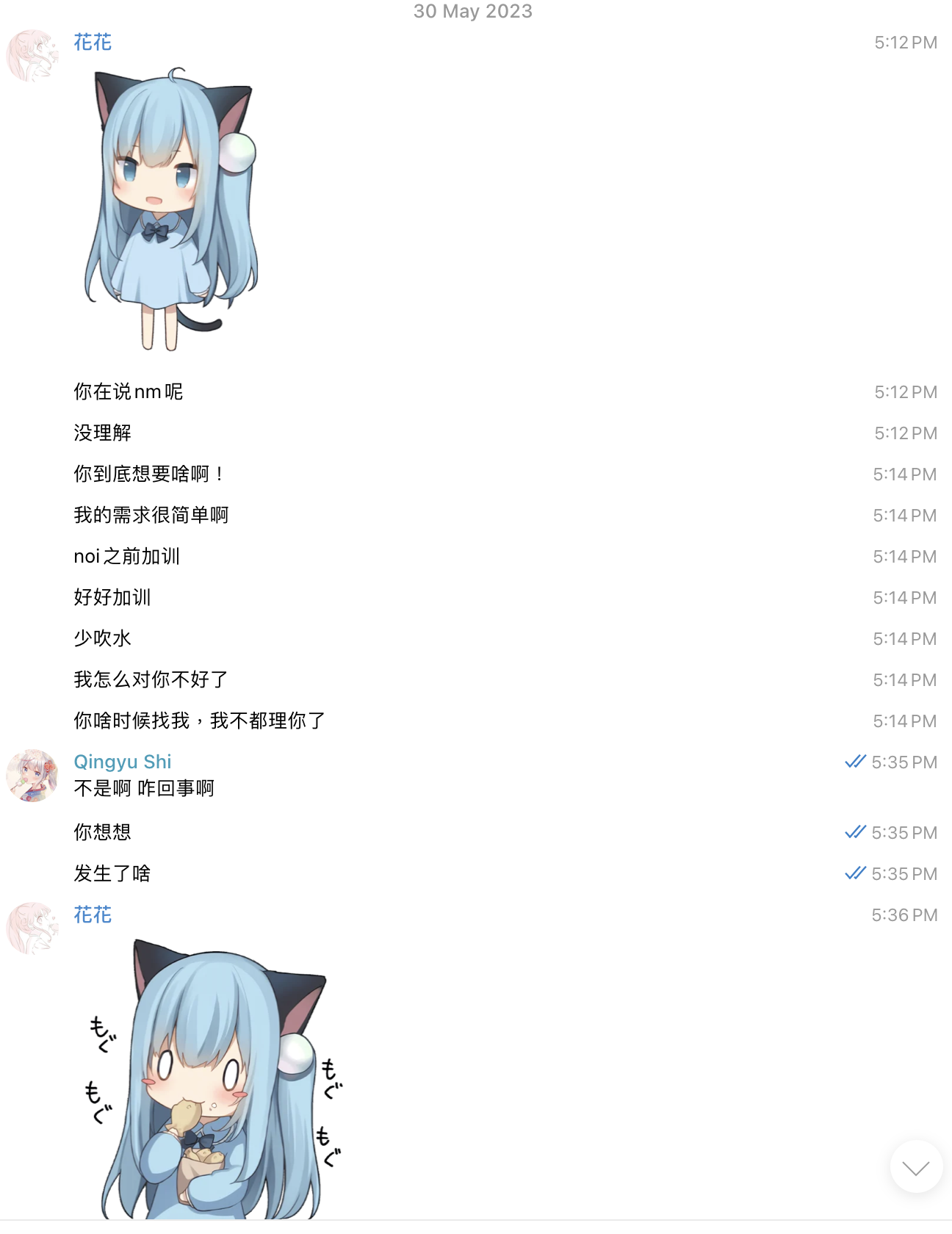
(4) CCPC Finals 小作文
2022 年的中国大学生程序设计竞赛决赛(CCPC Finals 2022)在 2023 年 5 月 15 日举办。当时,在杜老师的邀请下,我成为了比赛命题组的一员,参与了这套题目的命制与裁判工作。
而针对这场比赛,花花同学曾在知乎上写下了这样一篇小作文(在我发出这篇博客之时,此回答已被删除)
花花口中的 D 题,便是 Flower's Land 2。花花在自己的回答中声称
赛后交流了一下,发现我H的做法比出题人简单很多,也就成为了讲题ppt里的做法。然后d题要换,我就正好把屯了的idea扔了过去。 D其实是在脑子里很久的一个idea,在报道前两天晚上忽然说缺题了就把这个题跟杜老师说了说,幸运的成为了最后一个确定的ccpcf题。当晚就开始狂暴造题,为了能赶上第二天的验题队。
针对 “我H的做法比出题人简单很多,也就成为了讲题ppt里的做法” —— 最终讲题 PPT 的做法是戴江齐给出的,而且让戴老师写题解他还不写,彻底没法要了戴老师。整个做法的基础与 New Equipments III 相同(值得一提的是,这场 Bytedance Finals 在很长一段时间内都没有公开,还是我 py 了一个账号带花花打的比赛)。不过嘛,花花自己有这种做法,认为是 “成为了讲题ppt里的做法”,倒也能够理解,无可厚非。
但是花花自称 “然后d题要换,我就正好把屯了的idea扔了过去”,以及 “当晚就开始狂暴造题,为了能赶上第二天的验题队”,实在是过于厚颜无耻。
当时,花子正在忙着自己的训练(以及,当然,给自己的女朋友过生日),而他又迫切希望自己的题能够被选入。因此,花花在一次我与他的语音通话中让我去跟杜老师推荐这道题,希望能够让这道题被选入比赛。在原先的 D 题被爆了(后来变成了 Be Careful 2)以后,最终这道题目被顺利选入了比赛之中。然后,花子便告诉我自己很忙,要我帮他造这个题。在 5 月 10 日夜里,花子与我通宵连麦,开始了造这个题的过程。
不出所料,这个题造到一半,花子的代码就倒闭了。随后,花子陷入了暴躁模式,狂暴问我应该怎么办。最终,花子率先一步退出了这个题的造题过程,让我自己看着办。
那天夜里,正好杜老师在北京街头随机游走寻找酒店,最后就只有我和杜老师在拯救这个题。这个题救活了以后,花子也没有参与哪怕一点的造题任务之中。整个题从题面到数据,一切工作,全部都由我一个人完成。



最让我觉得不可理喻的是 “虽然标只跑了400ms,但是还是开了4s。于是理所应当的被验题队的根号log干过去了,然后在我的怒喷下,这个题最后还是改成了 $n = 5 \times 10^5$,5s的样子”。亲爱的花子,你也清楚根本不是你自己在干活,甚至连改个数据范围,改个 generator,都还得是 “在我的怒喷下”。最关键的是,你在这里打嘴炮的时候,真的有考虑过哪怕自己亲自造一下数据,亲自测一下代码,亲自改一下时限吗?你的算法竞赛水平比我高得多,我自然不敢跟您争论对数据结构都理解。但我知道的是,在标算使用 $2 \times 2$ 的矩阵,加上 I/O 优化与其他常数优化的情况下,跑出了 400ms,你确定应该用这一份代码来设定时间限制吗?你在那里安排别人干活的时候,锐评数据造的烂的时候,作为你自己口中的为了赶上验题进度连夜造题的自己,为什么就不能自己来造哪怕一组数据,测试哪怕一组 constraint 吗?
(5) “你能不能好好给我造数据”
(6) “我进了集训队你给我这么训练,我把你好友删了”
第一次删好友
NOI 2023 期间的聊天记录
背叛

如我上面所讲,我们在两年前所定下的约定,在花子的嘴里,一句轻飘飘的对不起就可以当作一张白纸。在我收到这段消息的时候,我恰巧在 HZNU 的草坪上躺着发呆,于是我就干脆一翻身,抱着这片草地开始痛哭。这期间他给我发的所有的消息,我都尽我所能以我认为体面的方式进行了回复。
同样,我不会在这里做出主观的评价,请你来定夺这是不是一个正常人该说出来的话。
从 CTT 到 CTS
(1) 锐评 Universal Cup
(2) 怎么写集训队论文
(3) 你怎么不带我做 research?
(4) 我是这些题目的出题人
这段故事实在是过于离谱,导致我到今天也不能理解怎么能发生这种事情……
简单来说,花子干了一件极度学术不端的事情。他拿了别人投给他的题投给我们,并称这是其自己出的题,最终导致我们在不知情的情况下对题目产生了错误的判断。
这是我们在命制今年 EC-Final 时发生的事情。你可以思考一下,在一场正式比赛,隐瞒题目的来源使其成为正式赛题是一件多么恐怖的事情。所以在事发后,我们出题组赶紧与这个人进行了切割。
正如上文所提,我在 2023 年参与了 CCPC Finals 的命题并进行了现场裁判工作。花子对当时我没有提议带他去现场感到不满,并想要在下一次的 EC-Finals 与 CCPC Finals 的命题中前往现场。
同时,花子想要努力进入 IOI 2024 的中国国家队。在选拔方案中,国家队队员会被要求命制一道题目,作为作业的一部分(即 “集训队互测”)。因此,花子主观上想要参与命题工作,客观上也有命题任务需要参加。
首先加入战场的是花子的集训队互测 落日珊瑚。这道题目的 idea 的基础是我在 EC-Final 命题期间枚举出来的,本来打算出成一道签到题。
【一段聊天记录】
对不起,写到这里心情有点爆炸了,未来有空再写吧。

(5) 你有没有想要感谢的人?
2024 年 9 月 13 日更新:
本来自己情绪稳定了一点,不打算再继续写这个人的小作文了。直到今天发现自己被一位热心网友喷了,我还是把喷我的评论与回应在这里贴一下。
>
不明白花花做错什么了,就因为我把你当唯一的朋友对你好,你也得把我当唯一的朋友,对我秀尽恩爱,否则就是道德败坏? 甚至,爆掉之后还要在 IOI 的节骨眼发文,让圈内都来讨伐花花?这是什么朋友......
<
My Reply: 请问,我有攻击过这个人不理我之类的问题吗?我当然能够接受你不把我当唯一的朋友,甚至不把我当朋友,但你选择既当婊子又立牌坊,前脚骂完娘后脚又来找我帮忙,你觉得这是一个正常的人能做出来的事情吗?偷别人的题目来投,不给别人 credit,这种事情说成道德败坏已经够给面子了,本质上这就是学术不端。 至于我发文,还要怪我,那就更搞笑了。他本人向我承诺跟我道歉,换取我不要将他的事情公之于众。他自己不尊重他自己的承诺,难道我被欺负了我就只能忍着?一个人自己做过的事情,难道不敢向大家承认吗?圈内的人来讨伐他,是因为我攻击他,还是因为他自己做的事情?既然你不把我当朋友,对我的帮助视而不见甚至恶语相向,那我为什么还要把你当做我的朋友?
>
圈外人看完后表示,就是一段畸形的、一厢情愿的友情。
花花这边,讲真没啥问题,要说有也就是心直口快,以及一些沟通方式的选择。可以看到即便爆了之后,他也依然可以说出“青鱼对我水平帮助很大”,愿意私下处理,愿意给予道歉和祝福,很成熟的体现。
反观 Qingyu 这边,他交朋友的初衷,是“付出一切来维护这个我仅有的朋友的友谊”,所以“几乎所有的时间都在与花子聊天”,又是点外卖又是帮着出题的。这其实是个很大的隐患,因为他也会反过来要求花花把他视为唯一的、最好的朋友,来倾尽一切地对待他,稍有不如意就会“问罪”。比如,生日不理他了、把 motto 删了,让人感觉很难沟通。自然,后面组队、去THU的事,花花也不愿意和他去沟通了,导致了更大的分歧。
但他最大的问题,还是选择 IOI 的节骨眼,把这篇檄文爆出来,让圈内的人都来讨伐花花,让花花在比赛时还要承受来自 OI 圈的压力,好像在说“我不好,你也别想好”(那条评论,感觉像是花花的 npy 留的)。至此,他已经失去了作为朋友的任何包容性。
真朋友,永远在心里,不在面儿上。
<
My Reply: 我比较好奇,为什么你会觉得这是 “一些沟通方式的选择”。哪怕你认为花子的沟通方式是他自己说话的风格,我也不能理解在喷完我之后继续找我帮忙,不愿意给帮助自己的人致谢,甚至要对其恶语相向。也许我的性格有缺陷,但对不起,我到今天也不能接受,在要我帮忙完成他的互测题、解题报告甚至帮忙完成集训队论文的同时而不肯致谢。抛开人品不谈,这就是赤裸裸的学术不端。
我还是那句话,我不强求花子做我的朋友。作为当事人,如果你认为我和你的关系你不能接受,你在第一次违背我们的约定,删了我的好友以后,为什么还要把我加回来?为什么找到我的第一件事是问我能不能帮自己写集训队论文?为什么第一句话是拜托我能不能加入我们的出题组?为什么第一天就要问我要 QOJ 的管理员?嘴上说自己承受了多少多少的压力,到头来还是要利用我为自己做事,我攻击他难道他是冤枉的吗?
我觉得我的忍耐能力已经足够强大,但对不起,在 EC-Final 这种借别人的题来骗自己的 credit 的行为,这种拿正式比赛命题开玩笑,丝毫不尊重我们的比赛的行为,我无法理解,无法接受,也有责任将他的所作所为公之于众。
由于我最近比较忙,有一些重要的事情要做,不出意外的话短期应该不会更新了。