- 搬题人:
- 数字:gyh20
- 因子:Wu_Ren
- 移除石子:feecle6418
- 抓内鬼:p_b_p_b
- 异或序列:feecle6418
- 数圈圈:feecle6418
- 组题人:hehezhou
- 题解:gyh20, Wu_Ren, feecle6418, p_b_p_b
数字 (Div. 2 Only)
来源:AtCoder Beginner Contest 182 (https://atcoder.jp/contests/abc182/tasks/abc182_c)
Tutorial by gyh20.
做法 $1$:
直接搜索每一位是否删掉,时间复杂度可以做到 $2^{\log n}\log n$ 或者 $2^{\log n}$,这里的 $\log$ 是以 $10$ 为底的,可以通过。
Submission #56492 - Public Judge (pjudge.ac)
做法 $2$:
我们知道,一个数字能被 $3$ 整除,当且仅当其所有数位之和是 $3$ 的倍数,所以我们一定不会删数位是 $3$ 的倍数的这些位,同时也不会删三个 $\bmod 3$ 相同的位,同时也不会同时删 $\bmod 3=1$ 的和 $\bmod 3=2$ 的,这样我们就知道答案不超过 $2$。
于是求出所有数位上有多少个 $\bmod 3=1$,多少个 $\bmod 3=2$,分类讨论一下即可。
Submission #56801 - Public Judge (pjudge.ac)
因子 (Div. 2 Only)
来源:
- Petrozavodsk Summer 2020. Day 5: JAG Summer+ Opening Contest. Problem B. Non-Trivial Common Divisor
- ACM-ICPC Japan Alumni Group Summer Camp 2019. Problem B. Non-Trivial Common Divisor
- https://qoj.ac/contest/505/problem/1336
Tutorial by Wu_Ren.
容易知道 $k$ 取某个质数最优,开个桶统计每个质数的答案即可,复杂度 $O(\sum \sqrt{a_i}+\omega (a_i))$。
移除石子 (Div. 1 + Div. 2)
来源:
- Petrozavodsk Winter 2020. Day 4: Yandex Cup 2020. Problem H. Delete the Points
- https://qoj.ac/contest/444/problem/692
Tutorial by feecle6418.
算法一
对于前三个测试点,可以从左往右删,第 $i$ 次输出 $(4i,4i,4i-2,4i-2)$。
对于第四、五个测试点,可以从下往上删,按照纵坐标顺序,第 $i$ 次删掉排在第 $2i-1$ 位、第 $2i$ 位的点即可。
结合起来期望得分 $50$。
算法二
大胆猜想一定有解。
算法一中的讨论指引我们从边上开始删。
将所有点按照横坐标从小到大排序,相同的按照纵坐标从小到大排序。不妨在该顺序中从后往前删。设在该顺序下,最后一个点为 $X$,倒数第二个点为 $Y$,倒数第三个点为 $Z$。
但是不一定合法,我们分类讨论几种情况:
$X,Y$ 都是横坐标最大的点,这时靠右放个正方形,可以删掉 $X,Y$。
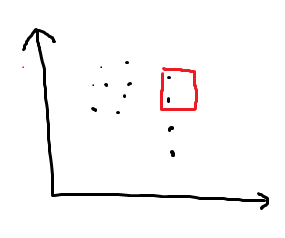
横坐标最大的点只有 $X$。
$Y$ 的纵坐标小于或等于 $X$ 的纵坐标,则放一个以 $Y$ 为左下顶点的很大的正方形。
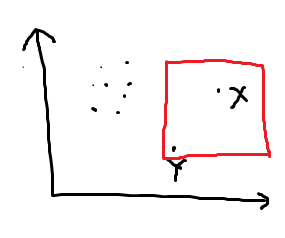
$Y$ 的纵坐标大于 $X$ 的纵坐标。
$Z$ 的横坐标等于 $Y$ 的横坐标,$Z$ 的纵坐标大于 $X$ 的纵坐标。
这时以 $YZ$ 为一边放一个正方形就可以删掉 $Y,Z$:
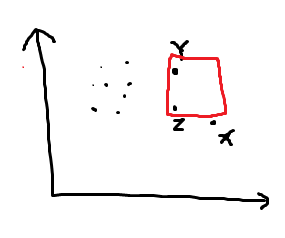
$Z$ 的横坐标等于 $Y$ 的横坐标,$Z$ 的纵坐标恰好等于 $X$ 的横坐标。
这时以 $YZ,ZX$ 中短的一边作为正方形的一条边,比如下图中 $YZ\le ZX$,就这样画:
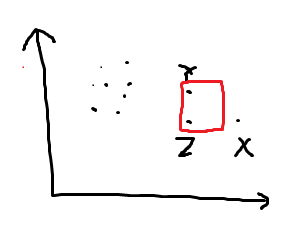
注意,为了防止 $YZ=ZX$ 时把 $XYZ$ 三个点恰好都框住,需要把正方形偏移 0.5 个单位,这也是题目允许输出小数的原因。
不是以上两种情况,则以 $(x_Y,y_X)$ 为左下角作一个很大的正方形即可:
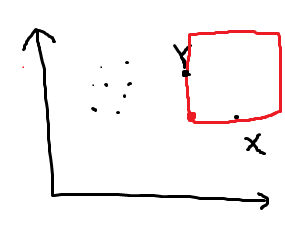
瓶颈在于排序,时间复杂度为 $O(n\log n)$,期望得分 $100$。
如果某些情况讨论漏了,可以得到 $90$ 分,因为数据随机时很难覆盖所有情况。
抓内鬼 (Div. 1 + Div. 2)
来源:
- Noric Collegiate Programming Contest 2021. Problem C. Customs Control
- Petrozavodsk Winter 2022. Day 4: Almost Northern Contest. Problem C. Customs Control
- https://qoj.ac/contest/822/problem/1774
Tutorial by p_b_p_b.
算法一
$k=1$ 。
不难想到一个简单策略是只在点 $1$ 处放一个 uoj 壮丁,其他地方都放 pjudge 壮丁。这种策略只会在 $1$ 和 $n$ 有边时失败,但此时唯一的最短路就是从 $1$ 一步走到 $n$ ,因此只要 $n\ge 3$ 就可以在 $1,n$ 都放 pjudge 壮丁,就解决了。
算法二
$u_i\in \{1,n\}$ 或 $v_i\in \{1,n\}$ 。
同样先特判掉 $1,n$ 有边的情况,然后不难发现只要给 $1$ 和 $n$ 分配不同来源的壮丁,剩下的点随便分,就一定可以掐断所有路线。或者如果 $k=0$ 或 $k=n$ 也是显然有解的。
算法三
一般情况。
沿用算法二,先给 $1,n$ 分配不同来源的壮丁,不妨假设 $1$ 的壮丁是 P 而 $n$ 的壮丁是 U 。
可以发现,如果存在边 $(1,x)$ ,并且 $x$ 的壮丁也是 P ,那就相当于把 $x$ 从图里删掉了。这是因为从 $1$ 不能一步走到 $x$ ,而其他拐一个弯再到 $x$ 的走法不可能是最短路。存在边 $(y,n)$ 且 $y$ 的壮丁是 U 的情况同理。
因此只需要把 pjudge 壮丁贪心分配给 $1$ 旁边的点。那么要么是把 $1$ 旁边的点都删完了,要么是剩下的 uoj 壮丁可以把 $n$ 旁边的点删完。总之 $1$ 和 $n$ 肯定有一个是周围的点被删完了。
异或序列 (Div. 1 Only)
来源:
- Petrozavodsk Winter 2021. Day 8: Belarusian SU Contest, Yandex Cup 2021. Problem C. Brave Seekers of Unicorns
- XXI Open Cup named after E.V. Pankratiev, Grand Prix of Belarus. Problem C. Brave Seekers of Unicorns
- https://qoj.ac/contest/536/problem/1085
Tutorial by feecle6418.
算法一
从小到大加入数来 dp。暴力一点,既然要求连续三个的异或和不为 $0$,就记录序列的最后两个位置 $x,y$ 分别是什么,加入 $z$ 的时候要求 $x,y,z$ 异或和不为 $0$。
时间复杂度 $O(n^3)$,期望得分 $40$ 分。
算法二
注意到性质:如果连续三个位置 $a_i,a_{i+1},a_{i+2}$ 违反了题目的限制,那 $(a_{i-1},a_i,a_{i+1})$ 就不可能违反限制了。
设 $f(n)$ 表示以 $n$ 结尾有多少个合法的序列。使用容斥:$f(n)=1+\sum _{i < n}f(i)-C$,$C$ 是在 $n$ 处第一次违反限制的序列数。$C$ 怎么算?如果一个序列 $[\dots,x,y,n]$ 在 $(x,y,n)$ 第一次违反限制,枚举 $y$,如果 $x=(y\operatorname{xor}n) < y$,$C$ 就应该加上 $f(x)$。
时间复杂度 $O(n^2)$,期望得分 $60$ 分。
算法三
对于 $\sum_{i < n}f(i)$ 这部分,可以用前缀和优化。
对于 $C=\sum_{y < n}[(y\operatorname{xor}n) < y]f(y\operatorname{xor}n)$,考虑满足条件的 $y$ 有何性质:实际上只要 $y$ 的二进制最高位和 $n$ 相同就有 $(y\operatorname{xor}n) < y$ 了。此时,枚举最高在哪一位 $y$ 和 $n$ 不同,则比这一位低的位可以任取,这样 $(y\operatorname{xor}n)$ 就属于一段特定的区间。因此我们把上述求和拆成了 $O(\log n)$ 段区间求和,同样可以前缀和。
时间复杂度 $O(n\log n)$,期望得分 $100$ 分。
数圈圈 (Div. 1 Only)
来源:
- Petrozavodsk Winter 2021. Day 8: Belarusian SU Contest, Yandex Cup 2021. Problem F. Border Similarity Undertaking
- XXI Open Cup named after E.V. Pankratiev, Grand Prix of Belarus. Problem F. Border Similarity Undertaking
- https://qoj.ac/contest/536/problem/1088
Tutorial by feecle6418.
算法一
枚举每种情况,再暴力判断条件是否满足。
可通过子任务 $1$,期望得分 $5$。
算法二
预处理从 $x$ 开始往右、往下最长的一段连续相同字符,再暴力枚举,这时可以 $O(1)$ 判断了。
时间复杂度 $O(n^2m^2)$,可通过子任务 $1,2$,期望得分 $15$。
算法三
子任务 $3$ 中,只需要求有多少个矩形,这很容易 $O(1)$ 计算。
子任务 $4$ 中,注意圈的大小肯定不大,因此小范围内枚举即可。结合前述期望得分 $40$。
算法四
考虑对矩阵分治,每次选择长的一边割开,然后计算经过中线(中线长度等于短的一边长度)的“圈”数量。不妨假设是竖着切的。
在下图中,我们对每一对 $(u,v)$ 求出左边的 匚 和右边对称的形状数量,最终乘起来即可。因为两边是对称的,下面就只描述怎么求 匚 数量了。
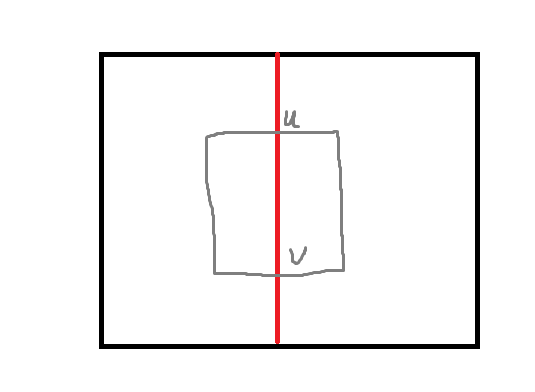
设 $L_u$ 表示 $u$ 往左,相同字符至多能延伸到第几列;$D_{x,y}$ 表示 $(x,y)$ 往下,相同字符至多能延伸到第几行。则我们要求的是 $$ \sum_{i=\max(L_u,L_v)}^{mid} [D_{i,u}\ge v] $$ 若 $L_u\ge L_v$,就是求: $$ \sum_{i=L_u}^{mid} [D_{i,u}\ge v] $$ 因为 $L_u$ 是固定的,所以这里可以用一个桶存下所有的 $D_{i,u}$,做个后缀和就可以 $O(1)$ 求出了。
否则,我们发现 $[D_{i,u}\ge v]$ 等价于 $[U_{i,v}\le u]$($U$ 表示向上延伸最远能到第几行),所以做法是一样的。
时间复杂度 $O(nm\log nm)$,因为递归有 $\log nm$ 层,设短边长 $x$ 长边长 $y$,每层用 $x^2+xy\le 2xy$ 也即 $O(xy)$ 的时间处理了询问,加起来每层是 $O(nm)$。可以通过本题得到 $100$ 分。
当然,如果固定 $u$ 将 $\{D_{i,u}\}$ 看成一个序列,上面就是问序列的某个后缀里有几个数 $\ge x$,用树状数组容易优化到 $O(\log n)$ 单次询问。时间复杂度 $O(nm(\log nm)^2)$。也可以通过本题得到 $100$ 分。