青鱼有一个平面直角坐标系。在 x 轴上有 $2n$ 个点,坐标从左到右分别为 $(0,0),(1,0),\dots,(2n-1,0)$。第 $i$ 个点 $(i-1,0)$ 的颜色为 $c_i$。对于每种 $1\le i\le n$,颜色 $i$ 恰好出现两次。
青鱼希望你在平面上画出 $n$ 条曲线,第 $i$ 条曲线连接两个颜色为 $i$ 的点,且曲线之间互不相交,且所有曲线都和以 $(0,0)$ 和 $(2n-1,0)$ 为端点的线段不相交(除了曲线端点处;注意,这意味着本题中 $n=1$ 时,直接用长度为 1 的线段连接 $(0,0),(1,0)$ 是非法的)。“不相交”就是没有公共点。(如果对相交的定义有疑问,可以阅读下发的 checker)
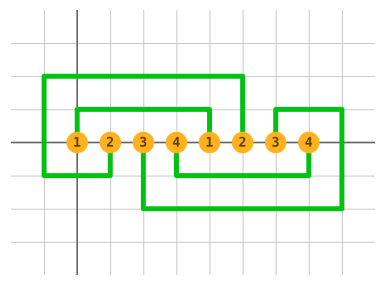
本题中,为了输出方便,我们认为“曲线”就是由几段平行于坐标轴,且端点横纵坐标都是整数的线段构成的,具体见输出格式。下图是一个例子:
输入格式
第一行一个正整数 $n$。
第二行 $2n$ 个正整数,第 $i$ 个为 $c_i$,表示 $(i-1,0)$ 的颜色。
输出格式
若存在连接方法,在第一行输出 YES。否则在第一行输出 NO。注意所有字母都是大写。
如果输出了 YES,还需要再输出 $n$ 行,第 $i$ 行按照如下格式输出:
- 假设颜色为 $i$ 的两个点分别为 $(x,0),(y,0)$,且 $x\lt y$。
- 第一个正整数为 $k$,表示连接 $(x,0),(y,0)$ 的曲线分为多少段。
- 接下来从 $(x,0)$ 开始,依次描述 $k$ 段线段,第 $i$ 段用一个字符(必须是
LRUD中的一个)和一个正整数 $z$ 描述,LRUD分别表示向左($(-1,0)$)右($(1,0)$)上($(0,1)$)下($(0,-1)$)方向,表示这条线段是从上一条线段的末尾(最初位置为 $(x,0)$ 开始)往该方向走 $z$ 长度。
具体请参考样例输出。你需要保证 $\sum k\le 2\times 10^6$,且所有输出的线段上任意一个点的坐标绝对值不超过 $10^8$。
如果输出了 YES 但是方案不正确,可以得到测试点 $40\%$ 的分数。注意,即使你不会输出方案,也需要输出一个符合格式的答案!
若输出了 NO,不用再输出其它东西。
样例
输入 1
4
1 2 3 4 1 2 3 4输出 1
YES
3 U 1 R 4 D 1
5 D 1 L 2 U 3 R 6 D 2
5 D 2 R 6 U 3 L 2 D 1
3 D 1 R 4 U 1该样例和题目描述中的图片是一样的。
下面给出了一个可以得到 $40\%$ 分数的输出:
YES
1 U 1
1 U 1
1 U 1
1 U 1输入 2
4
1 2 3 4 1 3 2 4输出 2
NO样例 3,4
见下发文件。注意,下发的输出文件只给出了 YES 或 NO,没有给出具体方案。
输出检查器
下发文件里的 checker.cpp 可以检查你的方案是否合法,但不会检查 YES 或 NO 是否正确。用法是将 checker.cpp 和 testlib.h 放于同一目录下编译得到可执行文件,可执行文件与输入文件 input 与输出文件 output 放于同一目录下,然后执行 checker input output output。
数据范围
本题捆绑测试。对于所有数据,$1\le n\le 2\times 10^5$,$1\le c_i\le n$,每种 $c_i$ 恰好出现两次。
性质 A:保证输出为 YES 的测试点都存在一种方案使得所有输出的曲线都不跨越 x 轴。
- 子任务 1($5$ 分)$n\le 2$。
- 子任务 2($5$ 分)$n\le 3$。
- 子任务 3($5$ 分)$n\le 4$。
- 子任务 4($5$ 分)$n\le 7$。
- 子任务 5($25$ 分)$n\le 1000$,性质 A。
- 子任务 6($25$ 分)$n\le 1000$。
- 子任务 7($10$ 分)性质 A。
- 子任务 8($20$ 分)无特殊限制。
时间限制:$1\texttt{s}$
空间限制:$1024\texttt{MB}$