给你一个包含 $n$ 个顶点和 $m$ 条边的无向图。每个顶点 $v$ 上写着一个数字 $a_v$,这个数字要么是 $0$,要么是 $1$。
一个路径(walk)指的是图中的一个顶点序列 $v_1 v_2 \dots v_k$,满足序列中相邻两个顶点之间都有一条边相连。
我们称一个二进制序列 $ s = s_1 s_2 \dots s_k $ 是可走的(walkable),当且仅当图中存在一条路径 $v_1 v_2 \dots v_k$,满足从这些顶点依次取出顶点上的数字得到的序列恰好等于 $s$,即:$a_{v_1} a_{v_2} \dots a_{v_k} = s$。换句话说,一个二进制序列是可走的,表示你可以通过在图中行走,并按顺序记录每个顶点上的数字,最终得到这个二进制序列。
一个例子如图所示。
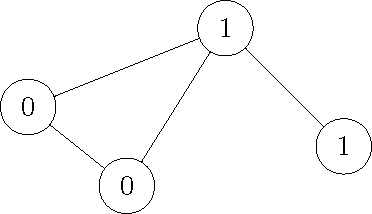
此例中,任意长度不超过3的二进制序列都是可走的。
你的任务是:求出最短的不可走二进制序列的长度。
输入格式
输入包含:
- 第一行两个整数 $n$ 和 $m$($1 \leq n \leq 3 \cdot 10^5$, $0 \leq m \leq 3 \cdot 10^5$),分别表示图的顶点数和边数。
- 第二行 $n$ 个整数 $a_1, a_2, \dots, a_n$(每个 $a_v \in {0, 1}$),表示第 $v$ 个顶点上的数字。
- 接下来 $m$ 行,每行两个整数 $u$ 和 $v$($1 \leq u, v \leq n$, $u \neq v$),表示顶点 $u$ 和顶点 $v$ 之间有一条边相连。输入保证任意两个顶点之间至多只有一条边。
输出格式
如果所有二进制序列都是可走的,输出“infinity”。
否则,输出最短的不可走二进制序列的长度。
样例数据
input
4 4 0 0 1 1 1 2 1 3 2 3 3 4
output
4
input
6 7 0 0 1 1 0 1 1 2 3 1 1 4 2 3 4 2 3 4 5 6
output
infinity
子任务
子任务一(7 分)
没有额外的限制。